题目内容
20.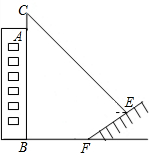 如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,某校有一教学楼AB,其上有一避雷针AC为7米,教学楼后面有一小山,其坡度为i=$\sqrt{3}$:1,山坡上有一休息亭供爬山人员休息,测得山坡脚F与教学搂的水平距离BF为19米,与休息亭的距离FE为10米,从休息亭E测得教学楼上避雷针顶点C的仰角为30°,求教学搂AB的高度.(结果保留根号)(注:坡度i是指坡面的铅直高度与水平宽度的比)
分析 如图作EN⊥BF,EM⊥BC垂足分别为N、M,在RT△EFN中求出EN,FN,在RT△CME中求出CM即可解决问题.
解答 解: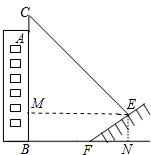 如图作EN⊥BF,EM⊥BC垂足分别为N、M.
如图作EN⊥BF,EM⊥BC垂足分别为N、M.
在RT△EFN中,∵∠ENF=90°,EF=10,EN:FN=$\sqrt{3}$,
∴tan∠EFN=$\sqrt{3}$,
∴∠EFN=60°,
∴FN=$\frac{1}{2}$EF=5,EN=$\sqrt{3}$FN=5$\sqrt{5}$,
∵∠MBN=∠EMB=∠ENB=90°,
∴四边形MENB是矩形,
∴BM=EN=5$\sqrt{3}$,ME=BN=BF+FN=24,
在RT△CME中,∠CME=90°,ME=24,∠CEM=30°,
∴CM=ME•tan30°=24×$\frac{\sqrt{3}}{3}$=8$\sqrt{3}$,
∴AM=CM-AC=8$\sqrt{3}$-7,
∴AB=AM+BM=8$\sqrt{3}$-7+5$\sqrt{3}$=(13$\sqrt{3}$-7)m.
∴教学搂AB的高度为(13$\sqrt{3}$-7)m.
点评 本题考查解直角三角形、仰角、俯角、坡度、特殊角的三角函数值等知识,解题的关键是理解这些概念,知道直角三角形已知一边一角即可解直角三角形,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.由4名同学每人写一个实系数一元二次方程,所得的四个方程中恰有两个无实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{8}$ |
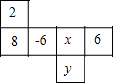 一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10.
一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10. 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.