题目内容
1.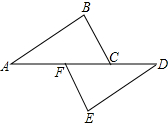 如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.
如图,点A、F、C、D在同一直线上,点B和E分别在直线AD的两侧,AB∥DE且AB=DE,AF=DC.求证:(1)AC=DF;
(2)BC∥EF.
分析 (1)根据等式的性质证明即可;
(2)根据已知条件得出△ACB≌△DEF,即可得出∠ACB=∠DFE,再根据内错角相等两直线平行,即可证明BC∥EF
解答 证明:(1)∵AF=DC,
∴AC=DF,
(2)∵AB∥DE,
∴∠A=∠D,
在△ABC与△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{∠A=∠D}\\{AC=DF}\end{array}\right.$,
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴BC∥EF.
点评 本题考查了全等三角形的判定和性质,关键是根据两直线平行的判定方法,内错角相等,两直线平行,难度适中.

练习册系列答案
相关题目
11.若两条平行直线被第三条直线所截,则( )
| A. | 一对同旁内角的角平分线互相垂直 | B. | 一对内错角的角平分线互相垂直 | ||
| C. | 一对同位角的角平分线互相垂直 | D. | 以上都不对 |
6.截止到2015年6月底,济南机动车总保有量为1640000辆,用科学记数法表示这个数为( )
| A. | 16.4×105 | B. | 1.64×105 | C. | 0.164×107 | D. | 1.64×106 |
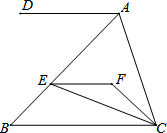 如图,∠DAC+∠ACB=180°,CE平分∠BCF,∠FEC=∠FCE,∠DAC=3∠BCF,∠ACF=20°.
如图,∠DAC+∠ACB=180°,CE平分∠BCF,∠FEC=∠FCE,∠DAC=3∠BCF,∠ACF=20°.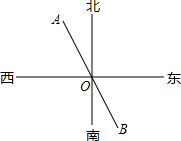 如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.
如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.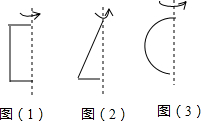
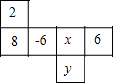 一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10.
一个正方体的相对的面上所标的两个数,都是互为相反数的两个数,如图是这个正方体的展开图,那么x+y的值为-10. 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.