Question

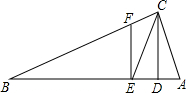如图，△ABC中，∠ACB=90°，CD⊥AB于D，CE平分∠ACB交AB于E，EF⊥AB．
（1）求证：EF∥CD；
（2）若∠A=65°，求∠FEC的度数．

Answer 1

考点：平行线的判定与性质,垂线

专题：证明题

分析：（1）根据垂线的定义得到∠CDB=∠FEB=90°，然后根据同位角相等，两直线平行即可得到EF∥CD；
（2）先根据角平分线的定义得∠ACE=45°，再利用互余计算出∠ACD=90°-∠A=25°，则∠ECD=∠ACE-∠ACD=20°，然后根据平行线的性质求解．

解答：（1）证明：∵CD⊥AB，EF⊥AB，
∴∠CDB=∠FEB=90°，
∴EF∥CD；
（2）解：∵∠ACB=90°，CE平分∠ACB交AB于E，
∴∠ACE=45°，
∵∠A=65°，
∴∠ACD=90°-65°=25°，
∴∠ECD=∠ACE-∠ACD=20°，
∵EF∥CD，
∴∠FEC=∠ECD=20°．

点评：本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．