题目内容
 如图,在梯形ABCD中,AD∥BC,BD⊥BC,且BD=BC=2AD,点E为AD的中点,连BE,对角线AC分别交BE、BD于点F、G.下列结论:
如图,在梯形ABCD中,AD∥BC,BD⊥BC,且BD=BC=2AD,点E为AD的中点,连BE,对角线AC分别交BE、BD于点F、G.下列结论:①DF平分∠ADB;②S△BDF=4S△DEF;③CF=4AF;④2S△CDG=5S△BFG,
其中正确的结论是( )
| A、①②③④ | B、①③④ |
| C、①②④ | D、②③ |
考点:相似三角形的判定与性质,角平分线的性质,梯形
专题:
分析:①过F作FM⊥AD于M,FN⊥BD于N,先根据平行线分线段定理求得FM=
BD,FN=
BD,然后根据到角的两边距离相等的点在角的平分线上即可求得结论,故①正确;
②根据EF:FB=1:4,△DEF和△BDF的高相等,即可证明结论,故②正确;
③根据平行线分线段定理即可证明结论,故③正确;
④由①可知FM=
BD,DG=
BD,得出BN=
BD,BG=
BD,设BD=BC=a,然后根据三角形面积公式求得S△BCF=
BC•BN=
×a×
a=
a2,S△BDC=
BC•BD=
a2,S△BCG=
BC•BG=
a•
a=
a2,然后用S△BDC-S△BCG,S△BCF-S△BCG求得△CDG和△BFG的面积,最后求得2S△CDG和5S△BFG的值即可得出结论,故④正确.
| 1 |
| 5 |
| 1 |
| 5 |
②根据EF:FB=1:4,△DEF和△BDF的高相等,即可证明结论,故②正确;
③根据平行线分线段定理即可证明结论,故③正确;
④由①可知FM=
| 1 |
| 5 |
| 1 |
| 3 |
| 4 |
| 5 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
解答: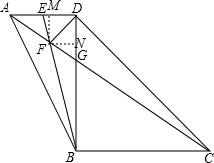 解:①、如图,过F作FM⊥AD于M,FN⊥BD于N,
解:①、如图,过F作FM⊥AD于M,FN⊥BD于N,
∵BD=BC=2AD,点E为AD的中点,
∴BD=BC=4AE=4ED,
∵AD∥BC,
∴AD:BC=DG:GC=1:2,AE:BC=AF:FC=EF:FB=1:4,
∴AF:AC=1:5,AG:AC=1:3,DG:BD=1:3,BF:EB=4:5
∴AF:AG=3:5,
∵FM⊥AD,FN⊥BD,BD⊥BC,
∴FM∥BD,FN∥AD,
∴FM:DG=AF:AG=3:5,FN:ED=BF:BE=4:5,
∵DG=
BD,ED=
BD,
∴FM=
BD,FN=
BD,
∴FM=FN,
∴DF平分∠ADB;
故①正确;
②、∵EF:FB=1:4,△DEF和△BDF的高相等,
∴S△BDF=4S△DEF,
故②正确;
③、∵AD∥BC,AE=
AD,BC=2AD,
∴AF:FC=AE:BC=1:4,
∴CF=4AF;
故③正确;
④、∵FM=
BD,DG=
BD
∴BN=
BD,BG=
BD,
设BD=BC=a,
∴S△BCF=
BC•BN=
×a×
a=
a2,S△BDC=
BC•BD=
a2,S△BCG=
BC•BG=
a•
a=
a2,
∴S△CDG=S△BDC-S△BCG=
a2,S△BFG=S△BCF-S△BCG=
a2,
∴2S△CDG=
a2,5S△BFG=
a2,
∴2S△CDG=5S△BFG,
故④正确;
故选A.
 解:①、如图,过F作FM⊥AD于M,FN⊥BD于N,
解:①、如图,过F作FM⊥AD于M,FN⊥BD于N,∵BD=BC=2AD,点E为AD的中点,
∴BD=BC=4AE=4ED,
∵AD∥BC,
∴AD:BC=DG:GC=1:2,AE:BC=AF:FC=EF:FB=1:4,
∴AF:AC=1:5,AG:AC=1:3,DG:BD=1:3,BF:EB=4:5
∴AF:AG=3:5,
∵FM⊥AD,FN⊥BD,BD⊥BC,
∴FM∥BD,FN∥AD,
∴FM:DG=AF:AG=3:5,FN:ED=BF:BE=4:5,
∵DG=
| 1 |
| 3 |
| 1 |
| 4 |
∴FM=
| 1 |
| 5 |
| 1 |
| 5 |
∴FM=FN,
∴DF平分∠ADB;
故①正确;
②、∵EF:FB=1:4,△DEF和△BDF的高相等,
∴S△BDF=4S△DEF,
故②正确;
③、∵AD∥BC,AE=
| 1 |
| 2 |
∴AF:FC=AE:BC=1:4,
∴CF=4AF;
故③正确;
④、∵FM=
| 1 |
| 5 |
| 1 |
| 3 |
∴BN=
| 4 |
| 5 |
| 2 |
| 3 |
设BD=BC=a,
∴S△BCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
∴S△CDG=S△BDC-S△BCG=
| 1 |
| 6 |
| 1 |
| 15 |
∴2S△CDG=
| 1 |
| 3 |
| 1 |
| 3 |
∴2S△CDG=5S△BFG,
故④正确;
故选A.
点评:本题考查了梯形的性质、平行线分线段定理,角的平分线的性质定理的逆定理,熟练掌握平行线分线段定理,角的平分线的性质定理的逆定理是本题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
在全国汉字听写大赛的热潮下,某学校进行了选拔赛,有15位学生进入了半决赛,他们的成绩各不相同,并且要按成绩取前8位进入决赛.小明只知道自己的成绩,要判断能否进入决赛,可用下列哪个统计结果判断( )
| A、平均数 | B、众数 |
| C、中位数 | D、方差 |
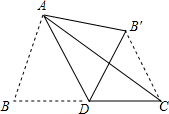 如图,△ABC中,BC=8,AD是中线,∠ADB=60°,将△ADB沿AD折叠至△ADB′,则点C到B′的距离是( )
如图,△ABC中,BC=8,AD是中线,∠ADB=60°,将△ADB沿AD折叠至△ADB′,则点C到B′的距离是( )| A、4 | ||
B、2
| ||
| C、3 | ||
D、2
|
∑表示数学中的求和符号,主要用于求多个数的和,∑下面的小字,i=1表示从1开始求和;上面的小字,如n表示求和到n为止.即
xi=x1+x2+x3+…+xn.则
(i2-1)表示( )
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| A、n2-1 |
| B、12+22+32+…+i2-i |
| C、12+22+32+…+n2-n |
| D、12+22+32+…+n2-(1+2+3+…+n ) |
不等式4-3x≥2x-6的非负整数解有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
某校学生的学习兴趣进行了一次抽样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣,B层次:较感兴趣,C层次:不感兴趣,并将调查结果绘制成了图①和图②的统计图(不完整),根据图中所给信息估计该校1200名学生中,C层次的学生约有( )


| A、360人 | B、180人 |
| C、30人 | D、1020人 |
一个多边形的每个内角不大于120°.那么这个多边形的边数最多是( )
| A、4 | B、6 | C、8 | D、10 |
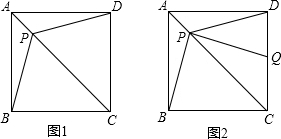
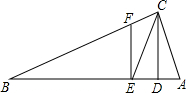 如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.
如图,△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB.