题目内容
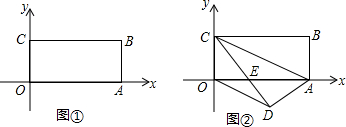
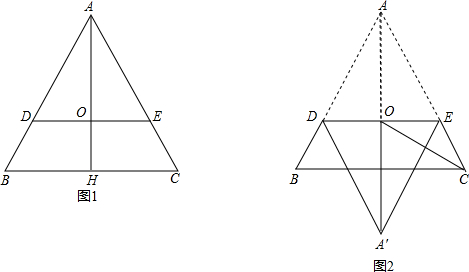
7.如图①,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别落在x,y轴上,且OA=8,OC=4.(1)直接写出点A,B,C的坐标;
(2)如图②,把矩形OABC沿对角线AC折叠,使点B落在点D处,且CD交x轴于点E,连结OD,那么下列说法中正确的有①②③
①△EDA≌△EOC;②∠ECA=∠EAC;③OD∥AC;④△COD是等腰三角形;⑤CD平分∠ACO
(3)求出图②中点E坐标;
(4)计算说四边形ODAC的面积.
分析 (1)根据OA和OC的长即可直接写出点的坐标;
(2)根据折叠的性质即可判断;
(3)证明△COE≌△ADE,得到EC=EA,在直角△OEC中,利用勾股定理即可列方程求解;
(4)过点D作DF⊥OA于点F,根据S四边形ODAC=S△AOC+S△AOD即可求解.
解答 解:(1)A的坐标是(8,0),B的坐标是(8,4),C的坐标是(0,4);
(2)正确的是:①②③;
(3)∵AB=AD,AB=OC,
∴AD=CO,
在△COE和△ADE中,
$\left\{\begin{array}{l}{∠AED=∠CEO}\\{∠COE=∠ADE}\\{AD=CO}\end{array}\right.$,
∴△COE≌△ADE,
∴EC=EA,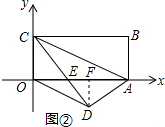
设OE=x,则EC=EA=8-x,
在直角△OEC中,OE2+OC2=EC2,x2+42=(8-x)2,
解得:x=3,
即E的坐标是(3,0).
(4)过点D作DF⊥OA于点F,则DF=$\frac{AD•DE}{AE}$=2.4,
则S四边形ODAC=S△AOC+S△AOD=$\frac{8×4}{2}$+$\frac{8×2.4}{2}$=16+9.6=25.6.
点评 本题考查了图形折叠的性质,以及全等三角形的判定与性质,正确理解折叠的性质,利用勾股定理求得OE的长是关键.

练习册系列答案
相关题目
12. 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
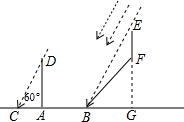 如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°
如图,小丽身高1.6米,此时太阳光线与地面的夹角为60°
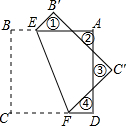 如图,正方形纸片ABCD的边长为4,将其沿EF折叠,则图中①②③④四个三角形的周长之和为16.
如图,正方形纸片ABCD的边长为4,将其沿EF折叠,则图中①②③④四个三角形的周长之和为16.