题目内容
11.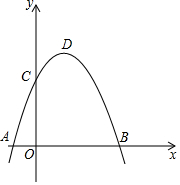 如图,抛物线y=-x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.
如图,抛物线y=-x2+bx+c过点B(3,0),C(0,3),D为抛物线的顶点.(1)求抛物线的解析式以及顶点坐标;
(2)如果点C关于抛物线y=-x2+bx+c对称轴的对称点为E点,连接BC,BE,求tan∠CBE的值;
(3)点M是抛物线对称轴上一点,且△DAM和△BCE相似,求点M坐标.
分析 (1)利用待定系数法求抛物线,然后把解析式配成顶点式,从而得到D的坐标;
(2)先利用抛物线的对称性得到E(2,3),作EH⊥BC于H,如图1,易得△OBC为等腰直角三角形得到∠OCB=45°,BC=$\sqrt{2}$OB=3$\sqrt{2}$,接着判断△CHE为等腰直角三角形得到CH=EH=$\frac{\sqrt{2}}{2}$CE=$\sqrt{2}$,所以BH=2$\sqrt{2}$,然后利用正切的定义求解;
(3)直线x=-1交x轴于F,如图2,解方程-x2+2x+3=0得A(-1,0),再利用正切定义得到tan∠AD=$\frac{1}{2}$,所以∠CBE=∠ADF,根据相似三角形的判定方法,当点M在点D的下方时,设M(1,m),当$\frac{DM}{BE}$=$\frac{DA}{BC}$时,△DAM∽△BCE;当$\frac{DM}{BC}$=$\frac{DA}{BE}$时,△DAM∽△BEC,于是利用相似比得到关于m的方程,解方程求出m即可得到对应的M点的坐标;当点M在D点上方时,则∠ADM与∠CBE互补,则可判断△DAM和△BCE不相似,
解答 解:(1)∵抛物线y=-x2+bx+c过点B(3,0),C(0,3),
∴$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线解析式为y=-x2+2x+3,
∵y=-x2+2x+3=-(x-1)2+4,
∴顶点D的坐标为(1,4);
(2)抛物线的对称轴为直线x=1,
∵点C与E点为抛物线上的对称点,
∴E(2,3),
作EH⊥BC于H,如图1,
∵OC=OB,
∴△OBC为等腰直角三角形,
∴∠OCB=45°,BC=$\sqrt{2}$OB=3$\sqrt{2}$,
∴∠ECB=45°,
∴△CHE为等腰直角三角形,
∴CH=EH=$\frac{\sqrt{2}}{2}$CE=$\sqrt{2}$,
∴BH=BC-CH=2$\sqrt{2}$,
在Rt△BEH中,tan∠EBH=$\frac{HE}{BH}$=$\frac{\sqrt{2}}{2\sqrt{2}}$=$\frac{1}{2}$,
即tan∠CBE的值为$\frac{1}{2}$;
(3)直线x=-1交x轴于F,如图2,
当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,则A(-1,0)
∵A(-1,0),D(1,4),
∴AF=2,DF=4,
∴tan∠ADF=$\frac{AF}{DF}$=$\frac{1}{2}$,
而tan∠CBE=$\frac{1}{2}$,
∴∠CBE=∠ADF,
AD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BE=$\sqrt{(3-2)^{2}+{3}^{2}}$=$\sqrt{10}$,BC=3$\sqrt{2}$,
当点M在点D的下方时,设M(1,m),
当$\frac{DM}{BE}$=$\frac{DA}{BC}$时,△DAM∽△BCE,
即$\frac{4-m}{\sqrt{10}}$=$\frac{2\sqrt{5}}{3\sqrt{2}}$,解得m=$\frac{2}{3}$,
此时M点的坐标为(1,$\frac{2}{3}$);
当$\frac{DM}{BC}$=$\frac{DA}{BE}$时,△DAM∽△BEC,
即$\frac{4-m}{3\sqrt{2}}$=$\frac{2\sqrt{5}}{\sqrt{10}}$,解得m=-2,
此时M点的坐标为(1,-2);
当点M在D点上方时,则∠ADM与∠CBE互补,则△DAM和△BCE不相似,
综上所述,满足条件的点M坐标为(1,$\frac{2}{3}$),(1,-2).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和相似三角形的判定与性质;会利用待定系数法求函数解析式;会利用相似比表示线段之间的关系;理解坐标与图形的性质,记住两点间的距离公式.

 阅读快车系列答案
阅读快车系列答案| A. | a≠-2 | B. | a>0 | C. | a≠0 | D. | a≠2 |
| A. | 1cm、2cm、3cm | B. | 3cm、4cm、6cm | C. | 1cm、1cm、3cm | D. | 2cm、3cm、7cm |
| 数据x | 70≤x≤79 | 80≤x≤89 | 90≤x≤99 |
| 个数 | 800 | 1300 | 900 |
| 平均数 | 78 | 85 | 92 |
| A. | 92 | B. | 85 | C. | 83 | D. | 78 |
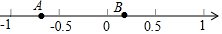 如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )
如图,在数轴上,点A和点B对应的数分别是a和b,考察结论:甲:-ab<$\frac{1}{2}$,乙:a+b>-1,丙:-a<b,丁:$\frac{a}{b}$>-2,其中正确的是( )| A. | 甲、乙 | B. | 甲、丙 | C. | 丙、丁 | D. | 乙、丁 |
| A. | 600x•2x=432 | B. | 600(1-x)•2x=432 | C. | 600(1-x)(1-2x)=432 | D. | 600(1-x)(1-x2)=432 |
| A. | x9 | B. | x6 | C. | x5 | D. | x |
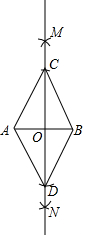 小明在白纸上作一个菱形,他按如下步骤:
小明在白纸上作一个菱形,他按如下步骤: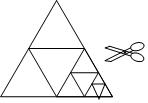 如图,将一张等边三角形纸片沿三边中点连线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,第七次操作后小三角形个数是( )
如图,将一张等边三角形纸片沿三边中点连线剪成4个小三角形,称为第一次操作;然后,将其中的一个三角形按同样方式再剪成4个小三角形,共得到7个小三角形,称为第二次操作;再将其中一个三角形按同样方式再剪成4个小三角形,共得到10个小三角形,称为第三次操作:…,根据以上操作,第七次操作后小三角形个数是( )