题目内容
1．要使分式$\frac{1}{2+a}$有意义，则a应满足的条件是（ ）| A． | a≠-2 | B． | a＞0 | C． | a≠0 | D． | a≠2 |
分析 根据分式有意义的条件即可求出a的取值范围．
解答 解：由题意可知：2+a≠0，
∴a≠-2
故选（A）
点评 本题考查分式有意义的条件，解题的关键是正确理解分式有意义的条件，本题属于基础题型．
练习册系列答案
相关题目
12．
如图所示，已知CD平分∠ACB，DE∥AC，∠1=30°，则∠2=（ ）
如图所示，已知CD平分∠ACB，DE∥AC，∠1=30°，则∠2=（ ）| A． | 35° | B． | 30° | C． | 50° | D． | 60° |
9．若a2-2a-2=0，则（a-1）2=（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
16．
如图，直线AB，CD交于O，EO⊥AB于O，若∠1=73°，则∠2等于（ ）
如图，直线AB，CD交于O，EO⊥AB于O，若∠1=73°，则∠2等于（ ）| A． | 27° | B． | 25° | C． | 23° | D． | 17° |
13．由$\frac{x}{3}$-y=6，可以得到用x表示y的式子是（ ）
| A． | x=18-y | B． | x=18-3y | C． | y=$\frac{x}{3}$-6 | D． | y=$\frac{x}{3}$+6 |
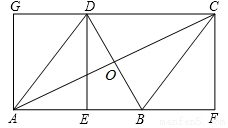如图，在矩形AFCG中，BD垂直平分对角线AC，交CG于D，交AF于B，交AC于O，连接AD，BC．
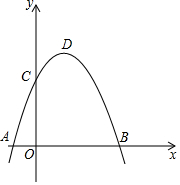如图，抛物线y=-x2+bx+c过点B（3，0），C（0，3），D为抛物线的顶点．