题目内容
6.若$\frac{2}{2{y}^{2}+3y+7}$=$\frac{1}{4}$,求$\frac{2}{4{y}^{2}+6y-1}$的值.分析 首先根据已知得出2y2+3y的值,再整体代入可得结果.
解答 解:∵$\frac{2}{2{y}^{2}+3y+7}$=$\frac{1}{4}$,
∴2y2+3y+7=8,
∴2y2+3y=1,
∴$\frac{2}{4{y}^{2}+6y-1}$=$\frac{2}{2({2y}^{2}+3y)-1}$=$\frac{2}{2×1-1}$=2.
点评 本题主要考查了分式的求值,整体代入是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.一次函数y=x-1的图象向上平移2个单位后,不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
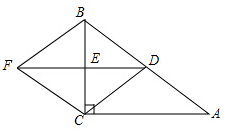 如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别是线段AB、BC的中点,连接DE,将△DBE沿直线BC翻折得△FBE,连接FC、DC. (1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=$\sqrt{2}$.
(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=$\sqrt{2}$.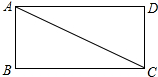 如图,在四边形ABCD中,AB=CD=6,BC=AD=8,AC=10.求证:四边形ABCD是矩形.
如图,在四边形ABCD中,AB=CD=6,BC=AD=8,AC=10.求证:四边形ABCD是矩形.