题目内容
1.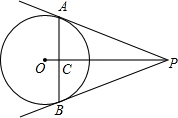 如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.(1)∠APO与∠BPO相等吗?为什么?
(2)OP与AB有怎样的关系?为什么?
分析 (1)连接OA,OB,可证明△OAP≌△OBP,从而得出∠APO与∠BPO相等;
(2)根据△OAP≌△OBP,得出PA=PB,根据等腰三角形的性质,得出OP垂直且平分AB.
解答  解:(1)∠APO与∠BPO相等,
解:(1)∠APO与∠BPO相等,
理由是:连接OA,OB,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
在Rt△OAP和Rt△OBP中,$\left\{\begin{array}{l}{OP=OP}\\{OA=OB}\end{array}\right.$,
∴Rt△OAP≌Rt△OBP(HL),
∴∠APO与∠BPO相等;
(2)∵△OAP≌△OBP,
∴PA=PB,
∵∠APO=∠BPO,
∴OP垂直且平分AB.
点评 本题考查了切线的性质以及全等三角形的判定,等腰三角形三线合一的性质,是重点,热点问题,要熟练掌握.

练习册系列答案
相关题目
11.已知P1(x1,y1)、P2(x2,y2)、P3(x3,y3)是反比例函数y=$\frac{10}{x}$的图象上的三点,且x1<x2<0<x3,则y1、2、y3的大小关系是( )
| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
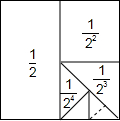 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.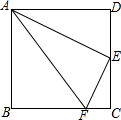 如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.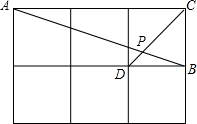 如图,在边长都为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,
如图,在边长都为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,