题目内容
11.已知a,b,c,d为实数,现规定一种运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc,那么当$|\begin{array}{l}{x+2}&{1}\\{2}&{x-1}\end{array}|$=8时,x为多少?分析 根据新定义得到(x+2)(x-1)-2=8,再把方程化为一般式得x2+x-12=0,然后利用因式分解法解方程求出x的值.
解答 解:根据题意得(x+2)(x-1)-2=8,
化为一般式得x2+x-12=0,
(x+4)(x-3)=0,
x+4=0或x-3=0,
所以x1=-4,x2=3,
即x的值为-4或3.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.下列数中,既是分数,又是正数的是( )
| A. | +3 | B. | -2$\frac{1}{4}$ | C. | 0 | D. | 2$\frac{3}{10}$ |
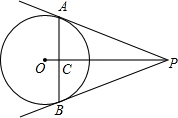 如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.