题目内容
11.已知P1(x1,y1)、P2(x2,y2)、P3(x3,y3)是反比例函数y=$\frac{10}{x}$的图象上的三点,且x1<x2<0<x3,则y1、2、y3的大小关系是( )| A. | y3<y2<y1 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y2<y3<y1 |
分析 先根据反比例函数图象上点的坐标特征求出y1=$\frac{10}{{x}_{1}}$,y2=$\frac{10}{{x}_{2}}$,y3=$\frac{10}{{x}_{3}}$,然后根据x1<x2<0<x3比较y1、2、y3的大小.
解答 解:∵P1(x1,y1)、P2(x2,y2)、P3(x3,y3)是反比例函数y=$\frac{10}{x}$的图象上的三点,
∴y1=$\frac{10}{{x}_{1}}$,y2=$\frac{10}{{x}_{2}}$,y3=$\frac{10}{{x}_{3}}$,
∵x1<x2<0<x3,
∴y2<y1<y3.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了解直角三角形.

练习册系列答案
相关题目
19.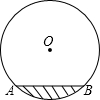 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
3.完成下列表格,并回答问题:
(1)
由表可知方程2x2-1=0的解在0与1之间.
(2)
由表可知方程2x2-1=0的解在0.7与0.8之间.
…
以此类推,求出方程2x2-1=0的近似解.(精确到0.01)
(1)
| x | 0 | 1 | 2 |
| 2x2-1 | -1 | 1 | 7 |
(2)
| x | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2x2-1 | -0.5 | -0.28 | -0.2 | 0.28 | 0.62 |
…
以此类推,求出方程2x2-1=0的近似解.(精确到0.01)
20.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的无盖纸盒.
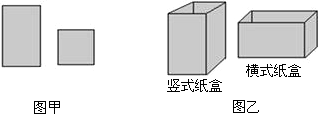
(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
②若这些纸板恰好用完,则可制作横式、竖式两种纸盒个多少个?
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.

(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.
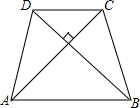 如图,等腰梯形ABCD的面积为100cm2,AC⊥BD.
如图,等腰梯形ABCD的面积为100cm2,AC⊥BD. 如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.