题目内容
9.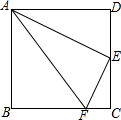 如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
如图,在正方形ABCD中,E是CD的中点,FC=$\frac{1}{4}$BC,则图中有3对相似三角形,△ADE与△AEF的周长比为2:$\sqrt{5}$.
分析 首先由四边形ABCD是正方形,得出∠D=∠C=90°,AD=DC=CB,又由DE=CE,FC=$\frac{1}{4}$BC,证出△ADE∽△ECF,然后根据相似三角形的对应边成比例与相似三角形的对应角相等,证明出△AEF∽△ADE,则可得△AEF∽△ADE∽△ECF,进而可得出结论.
解答 解:∵四边形ABCD是正方形,
∴∠D=∠C=90°,AD=DC=CB,
∵DE=CE,FC=$\frac{1}{4}$BC,
∴DE:CF=AD:EC=2:1,
∴△ADE∽△ECF,
∴AE:EF=AD:EC,∠DAE=∠CEF,
∴AE:EF=AD:DE,
即AD:AE=DE:EF,
∵∠DAE+∠AED=90°,
∴∠CEF+∠AED=90°,
∴∠AEF=90°,
∴∠D=∠AEF,
∴△ADE∽△AEF,
∴△AEF∽△ADE∽△ECF,
即△ADE∽△ECF,△ADE∽△AEF,△AEF∽△ECF,
设CF=x,则CE=DE=2x,
∴EF=$\sqrt{C{F}^{2}+C{E}^{2}}$=$\sqrt{5}$x,
∴△ADE与△AEF的周长比=$\frac{DE}{EF}$=$\frac{2x}{\sqrt{5}x}$=2:$\sqrt{5}$.
故答案为:3,2:$\sqrt{5}$.
点评 此题考查了相似三角形的判定与性质,以及正方形的性质,此题难度适中,解题的关键是证明△ECF∽△ADE,在此基础上可证△AEF∽△ADE.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
19.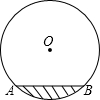 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
 在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )
在圆柱形油槽内装有一些油,截面如图,油面宽AB为6cm,如果再注入一些油后,油面上升1m,油面宽度为8m,圆柱形油槽的直径为( )| A. | 6m | B. | 8m | C. | 10m | D. | 12m |
20.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的无盖纸盒.
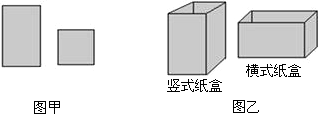
(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
②若这些纸板恰好用完,则可制作横式、竖式两种纸盒个多少个?
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.

(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.
 如图,A、B分别为y=ax2上两点,且线段AB⊥y轴于点(0,6),若AB=6,求该抛物线的表达式以及A、B坐标.
如图,A、B分别为y=ax2上两点,且线段AB⊥y轴于点(0,6),若AB=6,求该抛物线的表达式以及A、B坐标.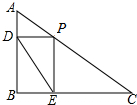 如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.
如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.
 如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C. 如图,点O是△ABC的两条角平分线的交点,过O作AO的垂线交AB于D,求证:△OBD∽△CBO.
如图,点O是△ABC的两条角平分线的交点,过O作AO的垂线交AB于D,求证:△OBD∽△CBO.