题目内容
12.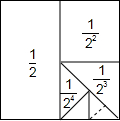 在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
在数学活动中,小明为了求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值(结果用n表示),设计如图所示的几何图形,请你利用这个几何图形求$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$的值为1-$\frac{1}{{2}^{n}}$.
分析 根据图形和正方形的面积公式分别求出$\frac{1}{2}$、$\frac{1}{2}$+$\frac{1}{{2}^{2}}$,从中找出规律,得到答案.
解答 解:$\frac{1}{2}$=1-$\frac{1}{2}$,
$\frac{1}{2}$+$\frac{1}{{2}^{2}}$=1-$\frac{1}{{2}^{2}}$,
…
$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}$+…+$\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$,
故答案为:1-$\frac{1}{{2}^{n}}$.
点评 本题考查的是图形的变化和数字的变化,根据图形和正方形的面积公式找出数字的变化规律是解题的关键.

练习册系列答案
相关题目
3.完成下列表格,并回答问题:
(1)
由表可知方程2x2-1=0的解在0与1之间.
(2)
由表可知方程2x2-1=0的解在0.7与0.8之间.
…
以此类推,求出方程2x2-1=0的近似解.(精确到0.01)
(1)
| x | 0 | 1 | 2 |
| 2x2-1 | -1 | 1 | 7 |
(2)
| x | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
| 2x2-1 | -0.5 | -0.28 | -0.2 | 0.28 | 0.62 |
…
以此类推,求出方程2x2-1=0的近似解.(精确到0.01)
20.某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方形形状的无盖纸盒.
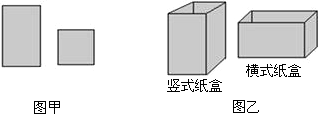
(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
②若这些纸板恰好用完,则可制作横式、竖式两种纸盒个多少个?
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.

(1)现有正方形纸板150张,长方形纸板300张,设做竖式纸盒x个,横式纸盒y个,
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) | |
| x | y | |
| 正方形纸板(张) | x | 2y |
| 长方形纸板(张) | 4x | 3y |
(2)若有正方形纸板32张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完,已知70<a<75.则a的值是73.
2.下列数中,既是分数,又是正数的是( )
| A. | +3 | B. | -2$\frac{1}{4}$ | C. | 0 | D. | 2$\frac{3}{10}$ |
 如图,A、B分别为y=ax2上两点,且线段AB⊥y轴于点(0,6),若AB=6,求该抛物线的表达式以及A、B坐标.
如图,A、B分别为y=ax2上两点,且线段AB⊥y轴于点(0,6),若AB=6,求该抛物线的表达式以及A、B坐标.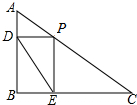 如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.
如图,在△ABC中,∠B=90°,AB=15cm,∠A=60°,动点P从点A开始沿AC点向C以2cm/s的速度移动(不与C重合),过点P作PD∥BC交AB于D,过P作PE∥AB交BC于E,若P点运动时间为t s.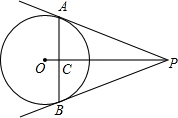 如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.
如图,PA、PB是⊙O的切线,切点分别为A、B,OP交AB于点C.