题目内容
16.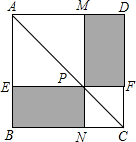 如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )
如图,在正方形ABCD中,P是线段AC上任意一点,过点P分别作EF∥AD,MN∥AB.设正方形AEPM和正方形CFPN的面积之和为S1,其余部分(即图中两阴影部分)的面积之和为S2,则S1与S2的大小关系是( )| A. | S1>S2 | B. | S1≥S2 | C. | S1<S2 | D. | S1≤S2 |
分析 先设正方形AEPM和正方形CFPN的边长为a和b,表示出S1与S2后比较即可.
解答 解:设正方形AEPM和正方形CFPN的边长为a和b,
则正方形AEPM和正方形CFPN的面积之和S1=a2+b2,
图中两阴影部分的面积之和S2=ab+ab=2ab,
把S1-S2=a2+b2-2ab=(a-b)2,
因为(a-b)2≥0,
所以可得S1≥S2,
故选B.
点评 此题考查完全平方公式,关键是两个面积的表示方法,注意用作差法比较.

练习册系列答案
相关题目
11.下列各式中,从等号左边变形至等号右边一定成立的是( )
| A. | $\frac{a+b}{{a}^{2}b}$=$\frac{ac+bc}{{a}^{2}bc}$ | B. | $\frac{2x}{{x}^{2}{+y}^{2}}$=$\frac{2x+1}{{x}^{2}{+y}^{2}+1}$ | ||
| C. | $\frac{2x}{{x}^{2}y+xy}$=$\frac{2}{xy+y}$ | D. | $\frac{{x}^{2}{+y}^{2}}{x+y}$=xy |
1.点A(3,-4)关于原点的对称点为( )
| A. | (3,4) | B. | (-3,4) | C. | (-3,-4) | D. | (4,3) |
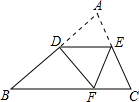 如图,D是AB边上的中点,DE∥BC,将△ABC沿过D的直线折叠,使点A落在BC上F处,
如图,D是AB边上的中点,DE∥BC,将△ABC沿过D的直线折叠,使点A落在BC上F处,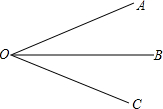 如图∠AOC=60°,OB是∠AOC的平分线,若再把∠AOB四等分,每一份是多少度角(精确到分)?
如图∠AOC=60°,OB是∠AOC的平分线,若再把∠AOB四等分,每一份是多少度角(精确到分)?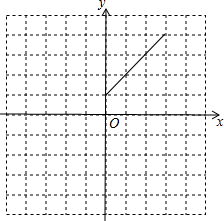 我们知道,把直线y=x向左平移1个单位可得到一次函数y=x+1的图象,把直线y=kx(k≠0)向左平移1个单位可得到一次函数y=k(x+1)的图象,把抛物线y=ax2(a≠0)向左平移1个单位,可得到二次函数y=a(x+1)2的图象.
我们知道,把直线y=x向左平移1个单位可得到一次函数y=x+1的图象,把直线y=kx(k≠0)向左平移1个单位可得到一次函数y=k(x+1)的图象,把抛物线y=ax2(a≠0)向左平移1个单位,可得到二次函数y=a(x+1)2的图象. 如图,在山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,则山高AB=50$\sqrt{3}$+50米.
如图,在山顶A望地面C、D两点,测得它们的俯角分别为45°和30°,已知CD=100米,则山高AB=50$\sqrt{3}$+50米.