题目内容
5.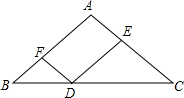 如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )
如图,在△ABC中,AB=AC=8,点D在BC上,DE∥AB,DF∥AC,则四边形AFDE的周长是( )| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
分析 因为AB=AC,所以△ABC为等腰三角形,由DE∥AB,可证△CDE为等腰三角形,同理△BDF也为等腰三角形,根据腰长相等,将线段长转化,求周长.
解答 解:∵AB=AC=15,
∴∠B=∠C,
由DF∥AC,得∠FDB=∠C=∠B,
∴FD=FB,
同理,得DE=EC.
∴四边形AFDE的周长=AF+AE+FD+DE
=AF+FB+AE+EC
=AB+AC
=8+8
=16.
故四边形AFDE的周长是16.
故选C.
点评 考查了等腰三角形的性质,本题利用了两直线平行,同位角相等和等边对等角及等角对等边来把四边形的周长转移到AB和ACH上求解的.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
15.将长度为3cm的线段向上平移10cm,再向右平移8cm,所得线段的长是( )
| A. | 3cm | B. | 8cm | C. | 10cm | D. | 无法确定 |
16.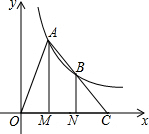 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
 如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A、B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,S△BNC=2,则k的值为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
13. 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )| A. | 40° | B. | 50° | C. | 140° | D. | 130° |
20.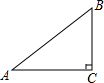 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
 如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )
如图,△ABC中,∠C=90°,则∠A的正弦值可以表示为( )| A. | $\frac{BC}{AB}$ | B. | $\frac{BC}{AC}$ | C. | $\frac{AC}{AB}$ | D. | $\frac{AC}{BC}$ |
10.菱形ABCD的边长为4,有一个内角为120°,则较长的对角线的长为( )
| A. | 4$\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
17.把抛物线y=-$\frac{1}{2}{x^2}$经( )平移得到y=-$\frac{1}{2}{(x-2)^2}$-1.
| A. | 向右平移2个单位,向上平移1个单位 | |
| B. | 向右平移2个单位,向下平移1个单位 | |
| C. | 向左平移2个单位,向上平移1个单位 | |
| D. | 向左平移2个单位,向下平移1个单位 |
14. 如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
 如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
如图,直线l1∥l2,等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )| A. | 35° | B. | 30° | C. | 25° | D. | 20° |
15.实数π,$\frac{\sqrt{5}-1}{2}$,0,3中是无理数的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |