题目内容
5．
如图，将△ABC沿直线DE折叠，使点C与点A重合，已知AB=7，BC=6，则△BCD的周长为13．
分析 利用翻折变换的性质得出AD=CD，进而利用AD+CD=AB得出即可．
解答 解：∵将△ABC沿直线DE折叠后，使得点A与点C重合，
∴AD=CD，
∵AB=7，BC=6，
∴△BCD的周长=BC+BD+CD=BC+BD+AD=BC+AB=7+6=13．
故答案为：13
点评 此题主要考查了翻折变换的性质，根据题意得出AD=CD是解题关键．
练习册系列答案
相关题目
15．
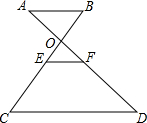如图，AB∥EF∥CD，BC、AD相交于点O，F是AD的中点，则下列结论中错误的是（ ）
如图，AB∥EF∥CD，BC、AD相交于点O，F是AD的中点，则下列结论中错误的是（ ）| A． | $\frac{AO}{AD}$=$\frac{BO}{BC}$ | B． | $\frac{OB}{CE}$=$\frac{OA}{DF}$ | C． | $\frac{EF}{CD}$=$\frac{OE}{BE}$ | D． | $\frac{2BE}{AD}$=$\frac{OE}{OF}$ |
13．
如图，直线a∥b，直线l与a、b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C，若∠1=58°，则∠2的度数为（ ）
如图，直线a∥b，直线l与a、b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C，若∠1=58°，则∠2的度数为（ ）| A． | 58° | B． | 42° | C． | 32° | D． | 28° |
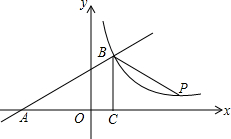如图，一次函数y=kx+b的图象与x轴交于点A，与反比例函数y=$\frac{m}{x}$（x＞0）的图象交于点B（2，n），过点B作BC⊥x轴于点C，点P（3n-4，1）是该反比例函数图象上的一点，且∠PBC=∠ABC，求反比例函数和一次函数的表达式．
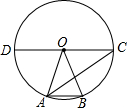如图，在⊙O中，A，B是圆上的两点，已知∠AOB=40°，直径CD∥AB，连接AC，则∠BAC=35度．
设函数y=$\frac{k}{x}$（k≠0，x＞0）的图象如图所示，若z=$\frac{1}{y}$，则z关于x的函数图象可能为（ ）
15．函数y=$\sqrt{x-4}$中自变量x的取值范围是（ ）
| A． | x≥0 | B． | x＞4 | C． | x＜4 | D． | x≥4 |