题目内容
20.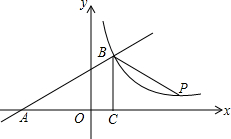 如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n-4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
分析 将点B(2,n)、P(3n-4,1)代入反比例函数的解析式可求得m、n的值,从而求得反比例函数的解析式以及点B和点P的坐标,过点P作PD⊥BC,垂足为D,并延长交AB与点P′.接下来证明△BDP≌△BDP′,从而得到点P′的坐标,最后将点P′和点B的坐标代入一次函数的解析式即可求得一次函数的表达式.
解答 解:∵点B(2,n)、P(3n-4,1)在反比例函数y=$\frac{m}{x}$(x>0)的图象上,
∴$\left\{\begin{array}{l}{2n=m}\\{3n-4=m}\end{array}\right.$.
解得:m=8,n=4.
∴反比例函数的表达式为y=$\frac{8}{x}$.
∵m=8,n=4,
∴点B(2,4),P(8,1).
过点P作PD⊥BC,垂足为D,并延长交AB与点P′.
在△BDP和△BDP′中,
$\left\{\begin{array}{l}{∠PBD=∠P′BD}\\{BD=BD}\\{∠BDP=∠BDP′}\end{array}\right.$
∴△BDP≌△BDP′.
∴DP′=DP=6.
∴点P′(-4,1).
将点P′(-4,1),B(2,4)代入直线的解析式得:$\left\{\begin{array}{l}{2k+b=4}\\{-4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=3}\end{array}\right.$.
∴一次函数的表达式为y=$\frac{1}{2}$x+3.
点评 本题主要考查的是一次函数和反比例函数的综合应用,根据题意列出方程组是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
10. 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为( )| A. | 45° | B. | 90° | C. | 100° | D. | 135° |
8.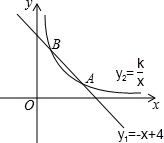 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(m,1),B(1,n)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(m,1),B(1,n)两点.
(1)求k,m,n的值;
(2)利用图象写出当x≥1时,y1和y2的大小关系.
 如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(m,1),B(1,n)两点.
如图,函数y1=-x+4的图象与函数y2=$\frac{k}{x}$(x>0)的图象交于A(m,1),B(1,n)两点.(1)求k,m,n的值;
(2)利用图象写出当x≥1时,y1和y2的大小关系.
15. 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
 如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )
如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为( )| A. | 2$\sqrt{3}$m | B. | 2$\sqrt{6}$m | C. | (2$\sqrt{3}$-2)m | D. | (2$\sqrt{6}$-2)m |
 如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为13.
如图,将△ABC沿直线DE折叠,使点C与点A重合,已知AB=7,BC=6,则△BCD的周长为13. 如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.
如图,△ABC是⊙O的内接三角形,AB为直径,过点B的切线与AC的延长线交于点D,E是BD中点,连接CE.