Question

15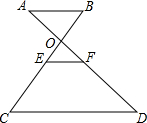．如图，AB∥EF∥CD，BC、AD相交于点O，F是AD的中点，则下列结论中错误的是（　　）

• A． $\frac{AO}{AD}$=$\frac{BO}{BC}$
• B． $\frac{OB}{CE}$=$\frac{OA}{DF}$
• C． $\frac{EF}{CD}$=$\frac{OE}{BE}$
• D． $\frac{2BE}{AD}$=$\frac{OE}{OF}$

Answer 1

分析 根据平行线分线段成比例定理，由AB∥CD得$\frac{AO}{AD}$=$\frac{BO}{BC}$，则可对A进行判断；先由AB∥EF得$\frac{OA}{OF}$=$\frac{OB}{OE}$，利用比例性质得$\frac{OB}{OA}$=$\frac{OE}{OF}$，由EF∥CD得$\frac{OE}{EC}$=$\frac{OF}{FD}$，利用比例性质得$\frac{OE}{OF}$=$\frac{EC}{FD}$，所以$\frac{OB}{OA}$=$\frac{EC}{FD}$，则可对B进行判断；由EF∥CD得$\frac{EF}{CD}$=$\frac{OE}{OC}$，则可对C进行判断；由EF∥CD得$\frac{OE}{EC}$=$\frac{OF}{FD}$，即$\frac{OE}{OF}$=$\frac{EC}{FD}$，加上F是AD的中点，则可对D进行判断．

解答 解：A、由AB∥CD得$\frac{AO}{AD}$=$\frac{BO}{BC}$，所以A选项的结论正确；
B、由AB∥EF得$\frac{OA}{OF}$=$\frac{OB}{OE}$，即$\frac{OB}{OA}$=$\frac{OE}{OF}$，由EF∥CD得$\frac{OE}{EC}$=$\frac{OF}{FD}$，即$\frac{OE}{OF}$=$\frac{EC}{FD}$，则$\frac{OB}{OA}$=$\frac{EC}{FD}$，即$\frac{OB}{EC}$=$\frac{OA}{DF}$，所以B选项的结论正确；
C、由EF∥CD得$\frac{EF}{CD}$=$\frac{OE}{OC}$，所以C选项的结论错误；
D、由EF∥CD得$\frac{OE}{EC}$=$\frac{OF}{FD}$，即$\frac{OE}{OF}$=$\frac{EC}{FD}$，而F是AD的中点，所以$\frac{OE}{OF}$=$\frac{2CE}{2DF}$，即$\frac{OE}{OF}$=$\frac{2BE}{AD}$，所以D选项的结论正确．
故选C．

点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．