题目内容
11.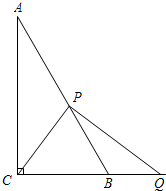 如图,在Rt△ABC中,∠C=90°,AB=6,P是射线AB上的一个动点,PQ⊥PC,交线段CB的延长线于点Q.
如图,在Rt△ABC中,∠C=90°,AB=6,P是射线AB上的一个动点,PQ⊥PC,交线段CB的延长线于点Q.(1)当BP=BC时,求证:BQ=BP;
(2)当点P在边AB上且∠A=30°时,设BP=x,BQ=y,求y关于x的函数解析式,并写出它的定义域;
(3)当∠A=30°,且BP=$\frac{5}{2}$时,请直接写出BQ的长.
分析 (1)根据等腰三角形的两个底角相等推知∠BPC=∠BCP;然后由垂直的定义、等量代换证得∠BPQ=∠BQP.易证结论;
(2)作PH⊥BC,垂足为点H.通过解直角△ABC知∠ABC=60°,BC=3.则根据图示与勾股定理求得,PH2+QH2=CQ2-(PH2+CH2),即2PH2+QH2=CQ2-CH2.所以将有关线段的长度代入其中,即可得到y与x的关系式.
解答 (1)证明:∵BP=BC,
∴∠BPC=∠BCP.
∵PQ⊥PC,
∴∠BPC+∠BPQ=90°,∠BCP+∠BQP=90°.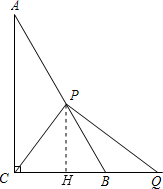
∴∠BPQ=∠BQP.
∴BQ=BP;
(2)解:作PH⊥BC,垂足为点H.
∵∠ACB=90°,∠A=30°,AB=6,
∴∠ABC=60°,BC=3.
∵BP=x,
∴BH=$\frac{x}{2}$,PH=$\frac{\sqrt{3}}{2}$x.
∴CH=3-$\frac{x}{2}$.
∵PQ2=PH2+QH2,PQ2=CQ2-CP2=CQ2-(PH2+CH2),
∴PH2+QH2=CQ2-(PH2+CH2),
即2PH2+QH2=CQ2-CH2.
∴2×($\frac{\sqrt{3}}{2}$x)2+(y+$\frac{x}{2}$)2=(y+3)2-(3-$\frac{x}{2}$)2.
整理,得xy-6y=3x-2x2,
∴所求的函数解析式为y=$\frac{2{x}^{2}-3x}{6-x}$.
定义域为1.5<x<6.
(3)解:当BP=$\frac{5}{2}$时,则x=$\frac{5}{2}$,y=$\frac{2×(\frac{5}{2})^{2}-3×\frac{5}{2}}{6-\frac{5}{2}}$=$\frac{10}{7}$.
点评 本题考查了勾股定理,直角三角形的性质,以及列函数解析式,关键是掌握在直角三角形中,30度角所对的直角边是所对的斜边的一半.等角对等边.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案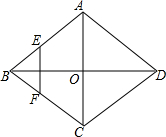 如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )
如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=$\sqrt{3}$,BD=4,则菱形ABCD的边长为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 7 |
| A. | 2:1 | B. | 3:1 | C. | 4:1 | D. | 5:1 |
 如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.
如图,在?ABOC中,对角线相交于点E,双曲线y=$\frac{k}{x}$(k<0)的一支经过C,E两点,若?ABCD的面积为10,求k的值.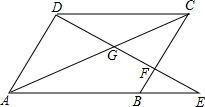 如图,四边形ABCD为平行四边形,试说明:
如图,四边形ABCD为平行四边形,试说明: 如图,在?ABCD中,E是AD上的一点,已知AE:ED=2:1,AO=4,求OC的长.
如图,在?ABCD中,E是AD上的一点,已知AE:ED=2:1,AO=4,求OC的长.