题目内容
如图在平面直角坐标系中,已知直角梯形OABC的顶点分别是O(0,0),点A(9,0),B(6,4).点P从点C沿C-B-A运动,速度为每秒2个单位,点Q从A向O点运动,速度为每秒1个单位,当其中一个点到达终点时,另一个点也停止运动.两点同时出发,设运动的时间是t秒.
(1)点C的坐标是( , );
(2)点P和点Q先到达终点是点 ;到达终点时t的值是 秒;
(3)当点P在线段BC上运动时,是否存在符合题意的t的值,使线段PQ=5?如果存在,求出t的值;如果不存在,请说明理由;
(4)当点P在线段BC上运动时,是否存在符合题意的t的值,使直角梯形OABC被直线PQ分成的两个部分面积之比为1:2?如果存在,求出t的值;如果不存在,请说明理由.
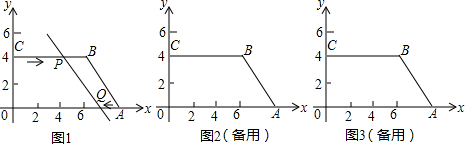
(1)点C的坐标是(
(2)点P和点Q先到达终点是点
(3)当点P在线段BC上运动时,是否存在符合题意的t的值,使线段PQ=5?如果存在,求出t的值;如果不存在,请说明理由;
(4)当点P在线段BC上运动时,是否存在符合题意的t的值,使直角梯形OABC被直线PQ分成的两个部分面积之比为1:2?如果存在,求出t的值;如果不存在,请说明理由.

考点:一次函数综合题
专题:
分析:(1)根据BC∥OA,即可求得C的坐标;
(2)求出BC,AB的长度,AQ的长度,即可求得从出发点到终点的时间;
(3)P从C到B所用的时间是:3秒,即可求得t的范围,作PD⊥OA于点D,在直角△PDQ中利用勾股定理即可列方程求得t的值;
(4)首先求得梯形ABCO的面积,根据直角梯形ABCO被直线PQ分成的两个部分面积之比为1:2,即可求得直角梯形QPCO的面积,利用时间t表示出直角梯形QPCO的面积,即可列方程求解.
(2)求出BC,AB的长度,AQ的长度,即可求得从出发点到终点的时间;
(3)P从C到B所用的时间是:3秒,即可求得t的范围,作PD⊥OA于点D,在直角△PDQ中利用勾股定理即可列方程求得t的值;
(4)首先求得梯形ABCO的面积,根据直角梯形ABCO被直线PQ分成的两个部分面积之比为1:2,即可求得直角梯形QPCO的面积,利用时间t表示出直角梯形QPCO的面积,即可列方程求解.
解答: 解:(1)C的坐标是(0,4);
解:(1)C的坐标是(0,4);
(2)AB=5,BC+BA=11,OA=9,
=5.5,
∴点P首先到达,到达的时间是5.5秒;
(3)P从C到B所用的时间是:
=3(秒),
在3秒内,Q从A到(6,0),则P一定在Q的左边.
设运动的时间是t秒,则CP=2t秒,AQ=t秒,
如图1,作PD⊥OA于点D,则D的坐标是(2t,0),PD=OC=4,
DQ=OA-OD-AQ=9-2t-t=9-3t,
在直角△PDQ中,PD2+DQ2=PQ2,即16+(9-3t)2=25,
解得:t=2或4(舍去).
故当t=2时,PQ=5;
(4)如图2.
∵A(9,0),B(6,4),
∴BC=6,OA=9,CO=4,
∴S直角梯形ABCO=
(BC+OA)•OC=
(6+9)×4=30,
设运动的时间是t秒,则CP=2t秒,AQ=t秒,则OQ=9-t,
则S梯形QPCO=
(PC+OQ)•OC=
(2t+9-t)×4=2t+18.
当S梯形QPCO=
S直角梯形ABCO=
×30=10时,2t+18=10,
解得:t=-4(舍去);
当S梯形QPCO=
S直角梯形ABCO=
×30=20时,2t+18=20,解得:t=1.
则当t=1时,直角梯形OABC被直线PQ分成的两个部分面积之比为1:2.
 解:(1)C的坐标是(0,4);
解:(1)C的坐标是(0,4);(2)AB=5,BC+BA=11,OA=9,
| 11 |
| 2 |
∴点P首先到达,到达的时间是5.5秒;
(3)P从C到B所用的时间是:
| 6 |
| 2 |
在3秒内,Q从A到(6,0),则P一定在Q的左边.
设运动的时间是t秒,则CP=2t秒,AQ=t秒,
如图1,作PD⊥OA于点D,则D的坐标是(2t,0),PD=OC=4,
DQ=OA-OD-AQ=9-2t-t=9-3t,
在直角△PDQ中,PD2+DQ2=PQ2,即16+(9-3t)2=25,
解得:t=2或4(舍去).
故当t=2时,PQ=5;
(4)如图2.
∵A(9,0),B(6,4),
∴BC=6,OA=9,CO=4,

∴S直角梯形ABCO=
| 1 |
| 2 |
| 1 |
| 2 |
设运动的时间是t秒,则CP=2t秒,AQ=t秒,则OQ=9-t,
则S梯形QPCO=
| 1 |
| 2 |
| 1 |
| 2 |
当S梯形QPCO=
| 1 |
| 3 |
| 1 |
| 3 |
解得:t=-4(舍去);
当S梯形QPCO=
| 2 |
| 3 |
| 2 |
| 3 |
则当t=1时,直角梯形OABC被直线PQ分成的两个部分面积之比为1:2.
点评:本题考查了直角梯形和列方程解应用题,正确利用时间t表示出图形中线段的长度以及梯形的面积是关键.

练习册系列答案
相关题目
 如图所示的正方体沿某些棱展开后,能得到的平面图形是( )
如图所示的正方体沿某些棱展开后,能得到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图,直线y=-
如图,直线y=- 在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C(-1,0),如图所示,过点B作BD⊥x轴,垂足为D,且点B横坐标为-3
在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C(-1,0),如图所示,过点B作BD⊥x轴,垂足为D,且点B横坐标为-3 (Ⅰ)一个三角形的内心是这个三角形的
(Ⅰ)一个三角形的内心是这个三角形的