Question

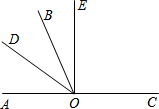如图所示，O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，∠BOE=

1

3

∠EOC．
（1）若∠AOD=30°，则∠BOE的度数为

 

°，在图中，与∠DOB互余的角有

 

，与∠DOB互补的角有

 

；
（2）若∠DOB=62°，求∠EOC的度数．

Answer 1

考点：余角和补角

专题：

分析：（1）根据角平分线的定义求出∠AOB，然后求出∠BOC，再求解即可得到∠BOE，然后根据互为余角的两个角的和等于90°，互为补角的两个角的和等于180°解答；
（2）根据角平分线的定义求出∠AOB，再求出∠BOC，然后求解即可．

解答：解：（1）∵OD平分∠AOB，
∴∠AOD=∠DOB=30°，
∠AOB=2∠AOD=2×30°=60°，
∴∠BOC=180°-60°=120°，
∵∠BOE=

1

3

∠EOC，
∴∠BOE=

1

1+3

×120°=30°，
∵∠AOB+∠BOE=60°+30°=90°，
∴∠DOB与互余的角是∠AOB，
∵∠DOB+∠COD=30°+（180°-30°）=180°，
∴∠DOB与∠COD互补；
故答案为：30，∠AOB，∠COD；

（2）∵OD平分∠AOB，
∴∠AOB=2∠AOD=2×62°=124°，
∴∠BOC=180°-∠AOB=180°-124°=56°，
∵∠BOE=

1

3

∠EOC，
∴∠EOC=

3

1+3

×56°=42°．

点评：本题考查了余角和补角，角平分线的定义，熟记概念并准确识图，理清图中各角度之间的关系是解题的关键．