题目内容
12．下列各式能用平方差公式计算的是（ ）| A． | （x+2y）（x-2y） | B． | （a+b）（a-2b） | C． | （-a+2b）（a-2b） | D． | （-2m-n）（2m+n） |
分析 可以用平方差公式计算的式子的特点是：两个二项式相乘，并且这两个二项式中有一项完全相同，另一项互为相反数．相乘的结果应该是：右边是乘式中两项的平方差（相同项的平方减去相反项的平方）．
解答 解：A、（x+2y）（x-2y）=x2-（2y）2=x2-4y2，能用平方差公式计算；
B、含a的项符号相同，而b与-2b不是互为相反数的项，不能用平方差公式计算；
C、含a、2b的项符号相反，不能用平方差公式计算；
D、含2m、n的项符号相反，不能用平方差公式计算．
故选A．
点评 本题考查了平方差公式，熟记公式结构是解题的关键．
练习册系列答案
相关题目
2．如图是用火柴棒摆出的一系列三角形图案，按这种方式摆下去，则所用的火车棒的根数y（根）与所摆图案的层数x（层）之间的关系可通过下表来探究．
每当所摆图案的层数x取一个定值时，所用火柴棒的根数y就随之确定，y与x的函数关系式是y=$\frac{3}{2}$x（x+1）．
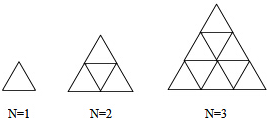
| x/层 | 1 | 2 | 3 | 4 | 5 | … |
| y/根 | 3 | 9 | 18 | 30 | 45 | … |
7．下列各式中计算正确的是（ ）
| A． | （x4）3=x7 | B． | （-a2）5=-a10 | C． | b5•b5=b25 | D． | a6÷a2=a3 |
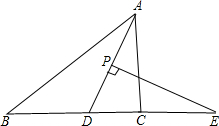如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．
一个几何体的三视图如图所示，根据图示的数据计算该几何体的全面积为8$\sqrt{3}$+72．