题目内容
17.先化简,再求值:已知(x+a)(x-$\frac{3}{4}$)的结果中不含关于字母x的一次项,求(a+2)2-(3-a)(-a-3)的值.分析 首先利用多项式的乘法法则计算:(x+a)(x-$\frac{3}{4}$),结果中不含关于字母x的一次项,即一次项系数等于0,即可求得a的值,然后把所求的式子化简,然后代入求值即可.
解答 解:(x+a)(x-$\frac{3}{4}$)
=x2+ax-$\frac{3}{4}$x-$\frac{3}{4}$a
=x2+(a-$\frac{3}{4}$)x-$\frac{3}{4}$a
由题意得a-$\frac{3}{4}$=0则a=$\frac{3}{4}$,
(a+2)2-(3-a)(-a-3)
=a2+4a+4+9-a2=4a+13,
当a=$\frac{3}{4}$时,原式=4×$\frac{3}{4}$+13=16.
点评 此题考查整式的化简求值,多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.

练习册系列答案
相关题目
7. 如图,是变压器中的L型硅钢片,其面积为( )
如图,是变压器中的L型硅钢片,其面积为( )
 如图,是变压器中的L型硅钢片,其面积为( )
如图,是变压器中的L型硅钢片,其面积为( )| A. | 4a2-b2 | B. | 4ab-b2 | C. | 4ab | D. | 4a2-4ab-b2 |
12.下列各式能用平方差公式计算的是( )
| A. | (x+2y)(x-2y) | B. | (a+b)(a-2b) | C. | (-a+2b)(a-2b) | D. | (-2m-n)(2m+n) |
2.已知?ABCD中,∠B=4∠A,则∠D=( )
| A. | 18° | B. | 36° | C. | 72° | D. | 144° |
6.观察下表多项式分解因式的特征,并回答问题.
对于二次项系数为1的二次三项式,若符合上述表中(2)(3)栏目的特征,就可以采用表中方法进行因式分解.
(1)分解因式:x2-4x-60;
(2)若x2+px-60可分解为两个一次因式的积,则整数p的值有12个.
| 1 | 2 | 3 | 4 |
| 多项式 | 常数项 | 一次项系数 | 分解因式 |
| x2+6x+8 | 8=2×4 | 6=2+4 | x2+6x+8=(x+2)(x+4) |
| x2-6x+8 | 8=(-2)×(-4) | -6=(-2)+(-4) | x2-6x+8=(x-2)(x-4) |
| x2+2x-8 | -8=4×(-2) | 2=4+(-2) | x2+2x-8=(x+4)(x-2) |
(1)分解因式:x2-4x-60;
(2)若x2+px-60可分解为两个一次因式的积,则整数p的值有12个.
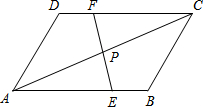 如图,?ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.
如图,?ABCD中,点E、F分别在AB、CD上,且BE=DF,EF与AC相交于点P,求证:PA=PC.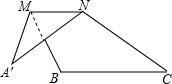 如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=30°,∠B=115°,则∠A′NC=110°.
如图,将△ABC沿它的中位线MN折叠后,点A落在点A′处,若∠A=30°,∠B=115°,则∠A′NC=110°.