题目内容
6. 二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号).
二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号).
分析 由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①∵抛物线的对称轴为x=1,a<0,
∴x≤1时,y随x的增大而增大,故正确;
②c>0,
∵-$\frac{b}{2a}$>0,
∴b>0,
∴abc<0,故此选项错误;
③当x=-1时,y=a-b+c<0,故a-b+c>0,错误;
④当x=2时,y=4a+2b+c>0,故正确;
⑤∵a<0,b>0,
∴3a-b<0,故此选项正确;
故答案为:①④⑤.
点评 本题考查了图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴和抛物线与y轴的交点、抛物线与x轴交点的个数确定.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16.某种品牌电风扇的标价为165元,若降价以九折出售,仍可获利10%(相对于成本价),那么该商品的成本价是( )
| A. | 115元 | B. | 125元 | C. | 135元 | D. | 145元 |
17.在平面直角坐标系中,点P(-2,3)关于y轴对称的点的坐标是( )
| A. | (3,-2) | B. | (2,-3) | C. | (-3,2) | D. | (2,3) |
 如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BD•cos∠HBD的值.
如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BD•cos∠HBD的值.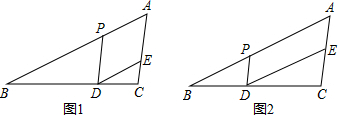

 如图,在一次数学活动课上,小明用18个棱长为1的正方体积木搭成一个几何体,然后他请小亮用其他棱长为1的正方体积木在旁边再搭一个几何体,使小亮所搭几何体恰好和小明所搭几何体拼成一个无空隙的大长方体(不改变小明所搭几何体的形状).
如图,在一次数学活动课上,小明用18个棱长为1的正方体积木搭成一个几何体,然后他请小亮用其他棱长为1的正方体积木在旁边再搭一个几何体,使小亮所搭几何体恰好和小明所搭几何体拼成一个无空隙的大长方体(不改变小明所搭几何体的形状).