题目内容
18. 等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A,C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.
等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A,C两点同时出发,均以1cm/秒的相同速度做直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D,设P点运动时间为t,△PCQ的面积为S.(1)求出S关于t的函数关系式.
(2)当点P运动几秒时,有S△PCQ=S△ABC.
分析 (1)由题可以看出P沿AB向右运动,Q沿BC向上运动,且速度都为1cm/s,S=$\frac{1}{2}$QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系;
(2)另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分条回答.
解答 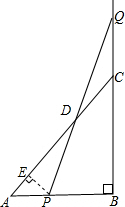 解:(1)过P点作PE⊥AC于E.
解:(1)过P点作PE⊥AC于E.
当t<10秒时,P在线段AB上,此时CQ=t,PB=10-t
∴s=$\frac{1}{2}$×t×(10-t)=$\frac{1}{2}$(10t-t2)
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t-10
∴s=$\frac{1}{2}$×t×(t-10)=$\frac{1}{2}$(t2-10t);
(2)∵S△ABC=$\frac{1}{2}$AB•BC=50,
∴当t<10秒时,S△PCQ=$\frac{1}{2}$(10t-t2)=50,
整理得t2-10t+100=0无解(6分)
当t>10秒时,S△PCQ=$\frac{1}{2}$(t2-10t)=50,
整理得t2-10t-100=0解得t=5±5$\sqrt{5}$(舍去负值),
∴当点P运动5+5$\sqrt{5}$秒时,S△PCQ=S△ABC.
点评 考查了一元二次方程的应用,做此类题应首先找出未知量与已知量的对应关系,利用已知量来表示未知量,许多问题就会迎刃而解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若平行四边形的一边长是12cm,则这个平行四边形的两条对角线长可以是( )
| A. | 5cm和7cm | B. | 20cm和30cm | C. | 8cm和16cm | D. | 6cm和10cm |
6.下表是汽车刹车后行驶的速度V1,路程S(m)与行驶的时间t(s)的一些数据,已知速度V1与时间t的函数关系是我们学习的两种函数(一次函数,二次函数)中的一种,路程S(m)是时间t(s)的二次函数.
(1)求速度V1与时间t的函数关系式,并求刚踩刹车时的速度V0;
(2)求路程S(m)与时间t(s)的函数关系式;
(3)汽车刹车后到停下来前进了多远?
| t(s) | 0.25 | 0.5 | 0.75 | 1 | 1.25 |
| V1(m/s) | 12 | 9 | 6 | 3 | 0 |
| S(m) | 3.375 | 6 | 7.875 | 9 | 9.375 |
(2)求路程S(m)与时间t(s)的函数关系式;
(3)汽车刹车后到停下来前进了多远?
13.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (-3pq)2=-6p2q2 | C. | (-bc)4÷(-bc)2=b2c2 | D. | a+a=a2 |
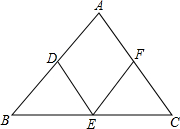 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,若添加一个条件,可以使四边形ADEF为菱形,你认为添加的条件可以是AB=AC.(只需要填写一个条件即可)
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,若添加一个条件,可以使四边形ADEF为菱形,你认为添加的条件可以是AB=AC.(只需要填写一个条件即可)