题目内容
8．设$\sqrt{3}$+1的整数部分是a，小数部分是b，a2+b2的值为8-2$\sqrt{3}$．分析 首先利用$\sqrt{3}$的取值范围得出a，b的值，进而利用完全平方公式求出即可．
解答 解：∵2＜$\sqrt{3}$+1＜3，
∴$\sqrt{3}$+1的整数部分是a=2，小数部分是b=（$\sqrt{3}$+1）-2=$\sqrt{3}$-1，
∴a2+b2=4+（$\sqrt{3}$-1）=8-2$\sqrt{3}$．
故答案为：8-2$\sqrt{3}$．
点评 此题主要考查了估算无理数的大小，得出a，b的值是解题关键．
练习册系列答案
相关题目
在等腰直角△ABC中，∠ACB=90°，D是AC中点，∠ADF=∠CDB，连接CF交BD于E，求证：BD⊥CF．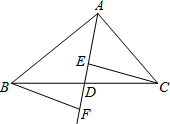
已知命题：如图，在△ABC中，点D是BC的点，作射线AD，在线段AD及其延长线上分别取点E、F，连结CE、BF，则△BDF≌△CDF，判断这个命题是真命题还是假命题？如果是真命题，请给出证明；如果是假命题，请添加一个适当的条件（不添加任何辅助线）使它成为真命题．你所添加的条件是：CE∥BF，并加以证明．
17．某种商品因换季准备打折出售，如果按规定价的七五折出售将赔25元，而按定价的九折出售将赚20元，问这种商品的定价是多少？设定价为x元，则下列方程中正确的是（ ）
| A． | $\frac{75}{100}$x-20=$\frac{9}{10}$x+25 | B． | $\frac{75}{100}$x+25=$\frac{9}{10}$x-20 | ||
| C． | $\frac{75}{100}$x-25=$\frac{9}{10}$x+20 | D． | $\frac{75}{100}$x+20=$\frac{9}{10}$x+25 |
等腰直角△ABC的直角边AB=BC=10cm，点P，Q分别从A，C两点同时出发，均以1cm/秒的相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D，设P点运动时间为t，△PCQ的面积为S．