题目内容
17.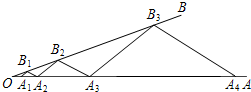 如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是32011.
如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是32011.
分析 根据面积比等于相似比的平方,从而可推出相邻两个三角形的相似比为1:3,面积比为1:9,先利用等底三角形的面积之比等于高之比可求出第一个及第二个三角形的面积,再根据规律即可解决问题.
解答 解:∵△A2B1B2和△A3B2B3的面积分别为1、9,A3B3∥A2B2,A3B2∥A2B1,
∴∠B1B2A2=∠B2B3A3,∠A2B1B2=∠A3B2B3,
∴△A2B1B2∽△A3B2B3,
∴$\frac{{A}_{2}{B}_{1}}{{A}_{3}{B}_{2}}$=$\frac{{B}_{1}{B}_{2}}{{B}_{2}{B}_{3}}$=$\frac{{A}_{2}{B}_{2}}{{A}_{3}{B}_{3}}$=$\sqrt{\frac{1}{9}}$=$\frac{1}{3}$,
∵A3B2∥A2B1,
∴△OA2B1∽△OA3B2,
∴$\frac{O{B}_{1}}{O{B}_{2}}$=$\frac{{A}_{2}{B}_{1}}{{A}_{3}{B}_{2}}$=$\frac{O{A}_{1}}{O{A}_{2}}$=$\frac{1}{3}$,
∴△OB1A2的面积为$\frac{1}{2}$,△A1B1A2的面积为$\frac{1}{3}$,△A2B2A3的面积为3,△A3B3A4的面积为27,…
∴△A1007B1007A1008的面积为$\frac{1}{3}$×32(1007-1)=32011,
故答案为32011.
点评 此题考查了相似三角形的判定与性质及平行线的性质,解答本题的关键是掌握相似比等于面积比的平方,及平行线分线段成比例,难度较大,注意仔细观察图形,得出规律.

练习册系列答案
相关题目
8.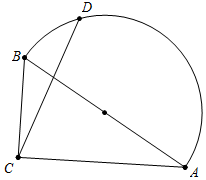 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
 如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )
如图,在Rt△ABC中,∠ACB=90°,tan∠CAB=$\frac{\sqrt{3}}{3}$,AB=3,点D在以斜边AB为直径的半圆上,点M是CD的三等分点,当点D沿着半圆,从点A运动到点B时,点M运动的路径长为( )| A. | π或$\frac{π}{2}$ | B. | $\frac{π}{2}$或$\frac{π}{3}$ | C. | $\frac{π}{3}$或π | D. | $\frac{π}{4}$或$\frac{π}{3}$ |
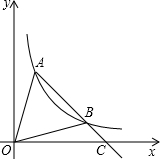 如图,A、B为反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,A、B两点坐标分别为(m,5-m)、(n,5-n)(m<n),连接AB并延长交x轴于点C.
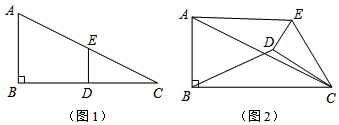
如图,A、B为反比例函数y=$\frac{k}{x}$(x>0)图象上的两点,A、B两点坐标分别为(m,5-m)、(n,5-n)(m<n),连接AB并延长交x轴于点C.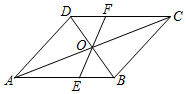 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.