题目内容
4.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,

第n次操作,分别作∠ABEn-1和∠DCEn-1的平分线,交点为En.
(1)如图①,求证:∠BEC=∠ABE+∠DCE;
(2)如图②,求证:∠BE2C=$\frac{1}{4}$∠BEC;
(3)猜想:若∠En=α度,那∠BEC等于多少度?(直接写出结论).
分析 (1)先过E作EF∥AB,根据AB∥CD,得出AB∥EF∥CD,再根据平行线的性质,得出∠B=∠1,∠C=∠2,进而得到∠BEC=∠ABE+∠DCE;
(2)先根据∠ABE和∠DCE的平分线交点为E1,运用(1)中的结论,得出∠CE1B=∠ABE1+∠DCE1=$\frac{1}{2}$∠ABE+$\frac{1}{2}$∠DCE=$\frac{1}{2}$∠BEC;同理可得∠BE2C=∠ABE2+∠DCE2=$\frac{1}{2}$∠ABE1+$\frac{1}{2}$∠DCE1=$\frac{1}{2}$∠CE1B=$\frac{1}{4}$∠BEC;
(3)根据∠ABE2和∠DCE2的平分线,交点为E3,得出∠BE3C=$\frac{1}{8}$∠BEC;…据此得到规律∠En=$\frac{1}{{2}^{n}}$∠BEC,最后求得∠BEC的度数.
解答  解:(1)如图①,过E作EF∥AB,
解:(1)如图①,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
(2)如图2,∵∠ABE和∠DCE的平分线交点为E1,
∴由(1)可得,
∠CE1B=∠ABE1+∠DCE1=$\frac{1}{2}$∠ABE+$\frac{1}{2}$∠DCE=$\frac{1}{2}$∠BEC;
∵∠ABE1和∠DCE1的平分线交点为E2,
∴由(1)可得,
∠BE2C=∠ABE2+∠DCE2=$\frac{1}{2}$∠ABE1+$\frac{1}{2}$∠DCE1=$\frac{1}{2}$∠CE1B=$\frac{1}{4}$∠BEC;
(3)如图2,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=$\frac{1}{2}$∠ABE2+$\frac{1}{2}$∠DCE2=$\frac{1}{2}$∠CE2B=$\frac{1}{8}$∠BEC;
…
以此类推,∠En=$\frac{1}{{2}^{n}}$∠BEC,
∴当∠En=α度时,∠BEC等于2nα度.
点评 本题主要考查了角平分线的定义以及平行线性质:两直线平行,内错角相等的运用.解决问题的关键是作平行线构造内错角,解题时注意:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

 寒假学与练系列答案
寒假学与练系列答案| A. | (2,2) | B. | (-2,-2) | C. | (2,-2) | D. | (-2,2) |
| A. | 开口向上,顶点坐标(3,1) | B. | 开口向下,顶点坐标(3,1) | ||
| C. | 开口向上,顶点坐标(-3,1) | D. | 开口向下,顶点坐标(-3,1) |
 如图,一长方形地块用来建造学校、小区、喷泉,求这块地的面积.
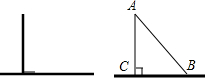
如图,一长方形地块用来建造学校、小区、喷泉,求这块地的面积. 为了减少交通事故的发生,“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70km/h.如图,一辆小汽车在一条由东向西的城市街道上直道行驶,某一时刻刚好行驶到路边车检测仪A处正前方50米的C处,过了4s后,测得小汽车所在的B处于车速检测仪的距离为130m,问这辆小汽车超速了吗?
为了减少交通事故的发生,“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70km/h.如图,一辆小汽车在一条由东向西的城市街道上直道行驶,某一时刻刚好行驶到路边车检测仪A处正前方50米的C处,过了4s后,测得小汽车所在的B处于车速检测仪的距离为130m,问这辆小汽车超速了吗? 如图,A、B.C为一个平行四边形的三个顶点,且A.B.C三点的坐标分别为(3,3)、(6,4)、(4,6).
如图,A、B.C为一个平行四边形的三个顶点,且A.B.C三点的坐标分别为(3,3)、(6,4)、(4,6). 小强从A到B共有三条路线:①A→B;②A→D→B;③A→C→B.在不考虑其他因素的情况下,我们可以肯定小明会走路线①.理由是两点之间,线段最短.
小强从A到B共有三条路线:①A→B;②A→D→B;③A→C→B.在不考虑其他因素的情况下,我们可以肯定小明会走路线①.理由是两点之间,线段最短.