题目内容
3.如图是用火柴棒摆出的图形,第一个图中有3根火柴棒和1个三角形,第二个图中有9根火柴棒和4个三角形,第三个图中有18根火柴棒和9个三角形…,则第10个图形中,火柴棒根数及三角形个数分别有( )
| A. | 165根、100个 | B. | 165根、55个 | C. | 135根、85个 | D. | 145根、100个 |
分析 由图得出第n个有1+3+5+…+2n-1=$\frac{n(2n-1+1)}{2}$=n2个三角形,共有3×(1+2+3+…+n)=$\frac{3}{2}$n(n+1)根火柴,由此代入求得答案即可.
解答 解:∵第一个图形有1个三角形,共有3×1根火柴;
第二个图形有1+3个三角形,共有3×(1+2)根火柴;
第三个图形有1+3+5个三角形,共有3×(1+2+3)根火柴;
…
∴第n个有1+3+5+…+2n-1=$\frac{n(2n-1+1)}{2}$=n2个三角形,共有3×(1+2+3+…+n)=$\frac{3}{2}$n(n+1)根火柴;
∴第10个图形中,火柴棒根数及三角形个数分别$\frac{3}{2}$×10×11=165,102=100.
故选:A.
点评 此题考查了图形的变化规律,解题的关键是发现三角形个数的规律,从而得到火柴棒的根数.

练习册系列答案
相关题目
15.在△ABC中,点D、E分别在AB、AC边上,∠B=∠AED,那么下列结论中不正确的是( )
| A. | AD:AC=AE:AB | B. | AD•AB=AE•AC | C. | DE:BC=AD:AC | D. | DE:BC=AD:AB |
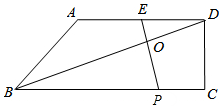 已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.
已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.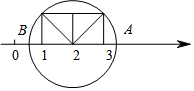 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画圆,与数轴相交.则圆与数轴的交点所表示的数是2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画圆,与数轴相交.则圆与数轴的交点所表示的数是2+$\sqrt{2}$或2-$\sqrt{2}$.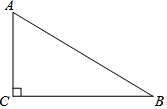 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.