题目内容
8. 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)用尺在边BC上求作一点P,使PA=PB,并连接AP;(不写作法,保留作图痕迹)
(2)当AC=3,AB=5时,△ACP的周长=7;
(3)当∠B为度时,AP平分∠CAB.
分析 (1)作AB的垂直平分线交BC于P点;
(2)先利用勾股定理计算出BC=4,然后利用PA=PB可得到△ACP的周长=AC+BC=7;
(3)利用PA=PB得到∠PAB=∠B,利用AP平分∠BAC得到∠CAP=∠BAP,则∠BAC=2∠B,然后根据三角形内角和可求出∠B的度数.
解答 解:(1)如图,点P为所作;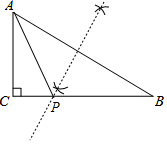
(2)在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵PA=PB,
∴△ACP的周长=AC+PC+AP=AC+CP+PB=AC+BC=3+4=7;
故答案为7;
(3)∵PA=PB,
∴∠PAB=∠B,
∵AP平分∠BAC,
∴∠CAP=∠BAP,
∴∠BAC=2∠B,
∵∠BAC+∠B=90°,
∴∠B=30°,
即∠B为30度时,AP平分∠CAB.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
18.从2开始,连续的偶数相加,它们和的情况如表:
(1)若n=8时,则和S的值为56;(直接填空,下同)
(2)根据表中的规律猜想:用n的代数式表示和S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)计算:34+36+38+…+108的值.
| 加数的个数n | 和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
(2)根据表中的规律猜想:用n的代数式表示和S的公式为:S=2+4+6+8+…+2n=n(n+1);
(3)计算:34+36+38+…+108的值.
19.已知函数y=x2+3x+c向右平移3个单位后过原点,那么c的值为( )
| A. | 0 | B. | -18 | C. | 3 | D. | -3 |
3.如图是用火柴棒摆出的图形,第一个图中有3根火柴棒和1个三角形,第二个图中有9根火柴棒和4个三角形,第三个图中有18根火柴棒和9个三角形…,则第10个图形中,火柴棒根数及三角形个数分别有( )


| A. | 165根、100个 | B. | 165根、55个 | C. | 135根、85个 | D. | 145根、100个 |