题目内容
13．先化简，再求值：（2a-1）2-（1-2a）（2a+1），其中a=-1．分析 先根据平方差公式和完全平方公式算乘法，合并同类项，最后代入求出即可．
解答 解：（2a-1）2-（1-2a）（2a+1）
=4a2-4a+1+4a2-1
=8a2-4a，
当a=-1时，
原式=8×（-1）2-4×（-1）=12．
点评 本题考查了整式的混合运算和求值，能正确根据整式的运算法则进行化简是解此题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
3．如图是用火柴棒摆出的图形，第一个图中有3根火柴棒和1个三角形，第二个图中有9根火柴棒和4个三角形，第三个图中有18根火柴棒和9个三角形…，则第10个图形中，火柴棒根数及三角形个数分别有（ ）
| A． | 165根、100个 | B． | 165根、55个 | C． | 135根、85个 | D． | 145根、100个 |
8．
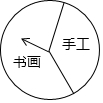某班“红领巾义卖”活动中设立了一个可以自由转动的转盘．规定：顾客购物20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：
（1）完成上述表格：a=295；b=0.745；
（2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“书画作品”的概率约是0.6；（结果全部精确到0.1）
（3）如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性，则表示“手工作品”区域的扇形的圆心角至少还要增加是多少度？
某班“红领巾义卖”活动中设立了一个可以自由转动的转盘．规定：顾客购物20元以上就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应的奖品．下表是此次活动中的一组统计数据：| 转动转盘的次数n | 100 | 200 | 300 | 400 | 500 | 1000 |
| 落在“书画作品”区域的次数m | 60 | 122 | 180 | 298 | a | 604 |
| 落在“书画作品”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | b | 0.59 | 0.604 |
（2）请估计当n很大时，频率将会接近0.6，假如你去转动该转盘一次，你获得“书画作品”的概率约是0.6；（结果全部精确到0.1）
（3）如果要使获得“手工作品”的可能性大于获得“书画作品”的可能性，则表示“手工作品”区域的扇形的圆心角至少还要增加是多少度？