题目内容
7.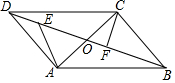 如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.
如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.(1)求线段EF的长;
(2)若△OAE的面积为S1,△OCF的面积为S2,S1+S2的值是否发生变化?若不变,求出这个不变的值;若变化,请说明随着DE的增大,S1+S2的值是如何发生变化的?
(3)求AE+CF的最小值.
分析 (1)根据平行四边形的性质得到OD=OB,于是得到结论;
(2)如图所示,连结AF,由四边形ABCD是平行四边形,得到AO=OC,求得S△AOF=S△COF,于是得到S1+S2=S△AEF=S△AOD,即可得到结论;
(3)当DE=OE时,AE+CF的值最小,此时E为OD的中点,于是得到结论.
解答 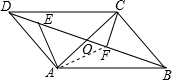 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴OD=OB,
∵DE=OF,
∴EF=OD=$\frac{1}{2}$BD=4;
(2)S1+S2的值不变,理由如下:
如图所示,连结AF,
∵四边形ABCD是平行四边形,
∴AO=OC,
∴S△AOF=S△COF,
∵DE=OF,
∴S△ADE=S△COF,
∴S1+S2=S△AEF=S△AOD,
∵∠BCO=90°,∠BOC=60°,
∴∠DAC=90°,∠AOD=60°,
∴AO=$\frac{1}{2}$OD=2,
在Rt△AOD中,AD=$\sqrt{3}$AO=2$\sqrt{3}$,
∴S1+S2=S△AOD=$\frac{1}{2}$AD•OA=$\frac{1}{2}$×2$\sqrt{3}$×2=2$\sqrt{3}$;
(3)当DE=OE时,AE+CF的值最小,此时E为OD的中点,
∵∠OAD=90°,
∴AE=$\frac{1}{2}$OD=2,
同理BQ=2,
∴AE+CF的最小值=4.
点评 本题是四边形综合题目,考查了平行四边形的性质、含30°角的直角三角形的性质、勾股定理、直角三角形斜边上的中线性质、三角形面积的计算等知识;本题难度较大,综合性强,特别是(2)(3)中,需要运用勾股定理、直角三角形斜边上的中线性质等知识才能得出结果.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
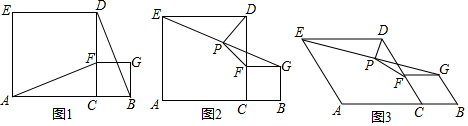
 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长. 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且3BO-$\frac{1}{2}$CO=1
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且3BO-$\frac{1}{2}$CO=1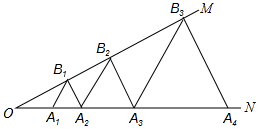 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.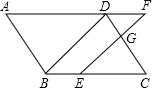 如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在平行四边形ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G. 如图,?ABCD中,AE平分∠BAD,若AB=5,CE=2,则?ABCD的周长是24.
如图,?ABCD中,AE平分∠BAD,若AB=5,CE=2,则?ABCD的周长是24.