题目内容
18. 如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.
如图,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点C时线段AB上一点,四边形OADC是菱形,求OD的长.
分析 由直线AB的解析式利用一次函数图象上点的坐标特征可得出点A、B的坐标,进而可得出OA、OB的长度,由OA、OB的长度利用勾股定理可求出AB的长度,根据菱形的性质可得出OE⊥AB、OE=DE,利用面积相等法可求出OE的长度,再根据OD=2OE即可求出OD的长度.
解答 解:∵直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,
∴点A(3,0),点B(0,4),
∴OA=3,OB=4,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5.
∵四边形OADC是菱形,
∴OE⊥AB,OE=DE,
∴$\frac{1}{2}$OA•OB=$\frac{1}{2}$OE•AB,即3×4=5OE,
解得:OE=$\frac{12}{5}$,
∴OD=2OE=$\frac{24}{5}$.
点评 本题考查了一次函数图象上点的坐标特征、菱形的性质、勾股定理以及三角形的面积,借用面积相等法求出OE的长度是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
10.下列说法正确的有( )
①-2是-4的一个平方根;
②a2的平方根是a;
③2是4的平方根;
④4的平方根是-2.
①-2是-4的一个平方根;
②a2的平方根是a;
③2是4的平方根;
④4的平方根是-2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,△ABC与△A′B′C′关于平行于y轴的一条直线对称,已知点A(1,2)关于这条直线的对称点A′的坐标为(-3,2),则点B(-2,-1)的对称点B′的坐标为(0,-1).
如图,△ABC与△A′B′C′关于平行于y轴的一条直线对称,已知点A(1,2)关于这条直线的对称点A′的坐标为(-3,2),则点B(-2,-1)的对称点B′的坐标为(0,-1).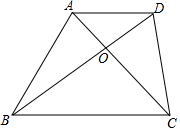 如图,梯形ABCD对角线交于O点,S△AOD=1,S△BOC=4,则S△AOB+S△DOC=( )
如图,梯形ABCD对角线交于O点,S△AOD=1,S△BOC=4,则S△AOB+S△DOC=( )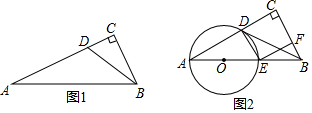
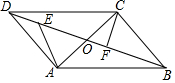 如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.
如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.