题目内容
15. 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且3BO-$\frac{1}{2}$CO=1
如图,直线y=kx-1与x轴、y轴分别交于B、C两点,且3BO-$\frac{1}{2}$CO=1(1)求点B的坐标及k的值;
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,在点A的运动过程中,试写出△AOB的面积S与x之间的函数解析式;
(3)探索:当点A运动到什么位置时,△AOB的面积是$\frac{1}{4}$?
分析 (1)利用坐标轴上点的坐标特征和一次函数图象上点的坐标特征先得到C(0,-1),B($\frac{1}{k}$,0),则利用3BO-$\frac{1}{2}$CO=1得到$\frac{3}{k}$-$\frac{1}{2}$=1,解方程得到k的值,从而得到B点坐标;
(2)A点坐标表示为(x,$\frac{1}{2}$x-1),然后利用三角形面积公式求解;
(3)设A(x,$\frac{1}{2}$x-1),利用三角形面积公式得到$\frac{1}{4}$|$\frac{1}{2}$x-1|=$\frac{1}{4}$,然后解绝对值方程得到x的值,从而得到A点坐标.
解答 解:(1)当x=0时,y=kx-1=-1,则C(0,-1),
当y=0时,kx-1=0,解得x=$\frac{1}{k}$,则B($\frac{1}{k}$,0),
∵3BO-$\frac{1}{2}$CO=1
∴$\frac{3}{k}$-$\frac{1}{2}$=1,
∴k=2,
∴B($\frac{1}{2}$,0);
(2)y=$\frac{1}{2}$x-1,
S=$\frac{1}{2}$•$\frac{1}{2}$•($\frac{1}{2}$x-1)
=$\frac{1}{8}$x-$\frac{1}{4}$(x>$\frac{1}{2}$);
(3)设A(x,$\frac{1}{2}$x-1),
∵S=$\frac{1}{2}$•$\frac{1}{2}$•|$\frac{1}{2}$x-1|,
∴$\frac{1}{4}$|$\frac{1}{2}$x-1|=$\frac{1}{4}$,解得x=4或x=0,
∴A点坐标为(4,1)或(0,1),
即A点运动到(4,1)或(0,1)位置时,△AOB的面积是$\frac{1}{4}$.
点评 本题考查了一次函数的综合题:熟练掌握一次函数图象上点的坐标特征;会求一次函数与坐标轴的交点坐标;理解坐标与图形的性质,记住三角形的面积公式.

 小学教材完全解读系列答案
小学教材完全解读系列答案①-2是-4的一个平方根;
②a2的平方根是a;
③2是4的平方根;
④4的平方根是-2.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
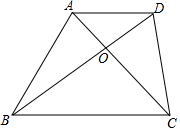 如图,梯形ABCD对角线交于O点,S△AOD=1,S△BOC=4,则S△AOB+S△DOC=( )
如图,梯形ABCD对角线交于O点,S△AOD=1,S△BOC=4,则S△AOB+S△DOC=( )
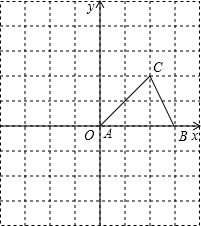 如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.
如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0)、C(2,2),将△ABC向左平移2个单位后再向下平移1单位,可得到△A′B′C′.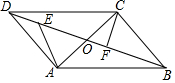 如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.
如图,点O为?ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(E,F不与端点重合),且DE=OF,连接AE,CF.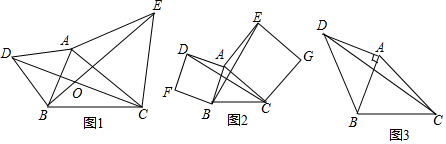
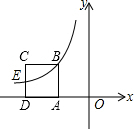 如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.
如图,正方形ABCD的边长为2,AD边在x轴负半轴上,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点B和CD边中点E,则k的值为-4.