题目内容
3.先化简,再求代数式$\frac{{x}^{2}-9{y}^{2}}{{x}^{2}y+2x{y}^{2}}$÷(x-2y-$\frac{5{y}^{2}}{x+2y}$)的值,其中x=tan60°,y=2sin30°.分析 先根据分式混合运算的法则把原式进行化简,再把x=3代入进行计算即可;
解答 解:原式=$\frac{{x}^{2}-9{y}^{2}}{xy(x+2y)}$÷$\frac{(x+2y)(x-2y)-5{y}^{2}}{x+2y}$
=$\frac{{x}^{2}-9{y}^{2}}{xy(x+2y)}$•$\frac{x+2y}{{x}^{2}-9{y}^{2}}$
=$\frac{1}{xy}$,
∵x=tan60°=$\sqrt{3}$,y=2sin30°=2×$\frac{1}{2}$=1,
∴原式=$\frac{1}{\sqrt{3}×1}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
8.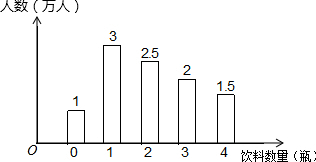 某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的60%.
表一
(2)试问A出口的被调查游客在园区内人均购买了多少瓶饮料?
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一所示 若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?
 某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的60%.
表一
| 出 口 | B | C |
| 人均购买饮料数量(瓶) | 3 | 2 |
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一所示 若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?
12.下列性质中,正方形具有而菱形不一定具有的性质是( )
| A. | 四条边相等 | B. | 对角线互相平分 | C. | 对角线相等 | D. | 对角线互相垂直 |
13.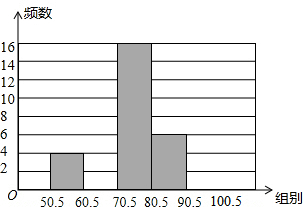 青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.
青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.
请根据图表,解答下面的问题:
(1)a=0.32,b=6,c=0.12,d=50;
(2)根据该样本,估计该校本次心理健康知识测试成绩在90分以上的人数;
(3)如果成绩在70分以上为心理健康状况良好,且心理健康状况良好的人数占总人数的70%以上,就表示该校学生的心理健康状况正常,否则就需要加强心理辅导.请根据上述数据分析该校学生是否需要加强心理辅导,并说明理由.
 青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.
青少年“心理健康”问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康”知识测试,并随机抽取了部分学生的成绩 (得分取正整数,满分为100分) 作为样本,绘制成如下尚未完成的频数分布表和频数分布直方图.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 14 | 0.28 |
| 70.5~80.5 | 16 | a |
| 80.5~90.5 | b | c |
| 90.5~100.5 | 10 | 0.2 |
| 合计 | d | 1.00 |
(1)a=0.32,b=6,c=0.12,d=50;
(2)根据该样本,估计该校本次心理健康知识测试成绩在90分以上的人数;
(3)如果成绩在70分以上为心理健康状况良好,且心理健康状况良好的人数占总人数的70%以上,就表示该校学生的心理健康状况正常,否则就需要加强心理辅导.请根据上述数据分析该校学生是否需要加强心理辅导,并说明理由.
 已知一次函数y=kx+b与x轴交于A点,与y轴交于B点,反比例函数y=-$\frac{k}{x}$(x>0)与直线AB只有一个交点,求S△AOB的值.
已知一次函数y=kx+b与x轴交于A点,与y轴交于B点,反比例函数y=-$\frac{k}{x}$(x>0)与直线AB只有一个交点,求S△AOB的值. 如图所示,D为等边△ABC内一点,△ABD经过旋转后到达△ACP的位置,旋转中心是哪一点,旋转角度是多少?
如图所示,D为等边△ABC内一点,△ABD经过旋转后到达△ACP的位置,旋转中心是哪一点,旋转角度是多少?