题目内容
8.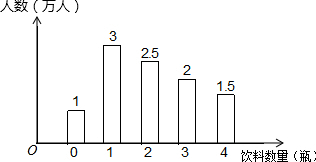 某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图(1)在A出口的被调查游客中,购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的60%.
表一
| 出 口 | B | C |
| 人均购买饮料数量(瓶) | 3 | 2 |
(3)已知B、C两个出口的被调查游客在园区内人均购买饮料的数量如表一所示 若C出口的被调查人数比B出口的被调查人数多2万,且B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,试问B出口的被调查游客人数为多少万?
分析 (1)根据条形统计图即可求得总人数和购买2瓶及2瓶以上的人数,从而求得购买2瓶及2瓶以上所占的百分比;
(2)根据加权平均数进行计算;
(3)设B出口人数为x万人,则C出口人数为(x+2)万人.根据B、C两个出口的被调查游客在园区内共购买了49万瓶饮料,列方程求解即可.
解答 解:(1)由图可知,购买2瓶及2瓶以上饮料的游客人数为2.5+2+1.5=6(万人),
而总人数为:1+3+2.5+2+1.5=10(万人),
所以购买2瓶及2瓶以上饮料的游客人数占A出口的被调查游客人数的$\frac{6}{10}$=60%,
故答案为:60.
(2)购买饮料总数位:3×1+2.5×2+2×3+1.5×4=3+5+6+6=20(万瓶).
人均购买瓶数:$\frac{20}{10}$=2(瓶).
(3)设B出口人数为x万人,则C出口人数为(x+2)万人.
则有3x+2(x+2)=49,解之得x=9.
所以B出口游客人数为9万人.
答:B出口的被调查游客人数为9万人.
点评 本题考查的是条形统计图的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
16.雾霾已经成为现在生活中不得不面对的重要问题,PM2.5是大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
| A. | 2.5×10-6 | B. | 0.25×10-6 | C. | 2.5×10-5 | D. | 0.25×10-5 |
13.化简:$\frac{\sqrt{2{5}^{2}-{7}^{2}}}{\sqrt{27}}$的结果是( )
| A. | $\frac{8\sqrt{6}}{3}$ | B. | $\frac{8\sqrt{3}}{9}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |