��Ŀ����
�������б���Ķ�Ӧֵ��

�жϷ��� ax2��bx��c=0(a��0��a��b��cΪ����)��һ����x��ȡֵ��Χ��( )
A. 3��x��3.23 B. 3��23��x��3.24 C. 3.24��x��3.25 D. 3.25��x��3.26
 C
����������������
����y=ax2+bx+c��ͼ����x��Ľ�����Ƿ���ax2+bx+c=0�ĸ�������y=ax2+bx+c��ͼ����x��Ľ����������Ϊ0��
�ɱ������ݿ�֪��y=0��y=��0.02��y=0.03֮�䣬���Ӧ��x��ֵ��3.24��3.25֮�䣬��3.24��x��3.25����ѡC��
C
����������������
����y=ax2+bx+c��ͼ����x��Ľ�����Ƿ���ax2+bx+c=0�ĸ�������y=ax2+bx+c��ͼ����x��Ľ����������Ϊ0��
�ɱ������ݿ�֪��y=0��y=��0.02��y=0.03֮�䣬���Ӧ��x��ֵ��3.24��3.25֮�䣬��3.24��x��3.25����ѡC��
 �Ķ��쳵ϵ�д�
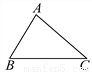
�Ķ��쳵ϵ�д���ͼ���ڡ�ABC�У���B�١�C.��֤��AB��AC.
 ������
��������������������ȼ���AB=AC���Ӷ��ó�����֪����ì�ܣ��Ӷ��ó��𰸣�
�������������AB=AC�� ���B=��C��������֪ì�ܣ���AB��AC��
������
��������������������ȼ���AB=AC���Ӷ��ó�����֪����ì�ܣ��Ӷ��ó��𰸣�
�������������AB=AC�� ���B=��C��������֪ì�ܣ���AB��AC�� ��ͼ��һ�߿�УΧǽ�������������ܳ�Ϊ40��������Χ��һ�����λ��ԣ������ABCD�ı�ABΪx�ף����ΪSƽ���ף�Ҫʹ����ABCD��������x�ij�Ϊ��������
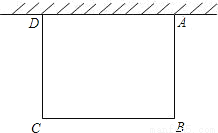
A. 10�� B. 15�� C. 20�� D. 25��
 A
�������������ABCD�ı�ABΪx�ף����Ϊ40-2x��
S=��40-2x��x= -2x2+40x��
Ҫʹ����ABCD������
��
��x�ij�Ϊ10m��
��ѡA��
A
�������������ABCD�ı�ABΪx�ף����Ϊ40-2x��
S=��40-2x��x= -2x2+40x��
Ҫʹ����ABCD������
��
��x�ij�Ϊ10m��
��ѡA�� ��ͼ����֪������y=-x2+bx+c��x�����������ֱ�ΪA(x1��0)��B(x2��0) �� ��x1+x2=4��  .
.
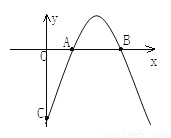
(1)�������ߵĴ�������ʽ;
(2)����������y�ύ��C�㣬��ֱ��BC�ı���ʽ;
(3)���ABC�����.
 ��1���������ߵĴ�������ʽΪy=-x2+4x-3����2��ֱ��BC�Ĵ�������ʽΪy=x-3����3��S��ABC=3.
�������������������1���Ƚⷽ����, ���x1��x2��ֵ���ٴ���������y=-x2+bx+c������������ߵĴ�������ʽ��
��2����ֱ��BC�ı���ʽΪy=kx+m���������������y��Ľ������꣬�ٸ��ݴ���ϵ�����������ֱ��BC�ı���ʽ��
��3���ֱ����AB��OC�ij����ٸ�...
��1���������ߵĴ�������ʽΪy=-x2+4x-3����2��ֱ��BC�Ĵ�������ʽΪy=x-3����3��S��ABC=3.
�������������������1���Ƚⷽ����, ���x1��x2��ֵ���ٴ���������y=-x2+bx+c������������ߵĴ�������ʽ��
��2����ֱ��BC�ı���ʽΪy=kx+m���������������y��Ľ������꣬�ٸ��ݴ���ϵ�����������ֱ��BC�ı���ʽ��
��3���ֱ����AB��OC�ij����ٸ�... ��֪���κ���y=��x2+2x+m�IJ���ͼ����ͼ��ʾ�������x��һԪ���η��̩�x2+2x+m=0�Ľ�Ϊ_____��

 x1=4��x2=��2
������������������ɶ��κ���y=��x2+2x+m�IJ���ͼ����Եõ������ߵĶԳ������������x���һ���������꣬Ȼ����������һ���������꣬��������������x�ύ��ĺ���������Ӧ��һԪ���η��̵ĸ��Ĺ�ϵ���ɵõ�����x��һԪ���η��̩�x2+2x+m=0�Ľ⣮
��������
������ö��κ���y=��x2+2x+m�ĶԳ���Ϊx=1����x���һ������Ϊ��3��0����
��������...
x1=4��x2=��2
������������������ɶ��κ���y=��x2+2x+m�IJ���ͼ����Եõ������ߵĶԳ������������x���һ���������꣬Ȼ����������һ���������꣬��������������x�ύ��ĺ���������Ӧ��һԪ���η��̵ĸ��Ĺ�ϵ���ɵõ�����x��һԪ���η��̩�x2+2x+m=0�Ľ⣮
��������
������ö��κ���y=��x2+2x+m�ĶԳ���Ϊx=1����x���һ������Ϊ��3��0����
��������... ��ͼ������ABCD�����߳�AB��18cm��AD��4cm.��P��Q�ֱ��A��Bͬʱ������P�ڱ�AB����AB������ÿ��2cm���ٶ������˶���Q�ڱ�BC����BC������ÿ��1cm���ٶ������˶������˶�ʱ��Ϊx�룬��PBQ�����Ϊy(cm2)��
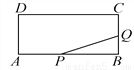
(1)��y����x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
(2)���PBQ����������ֵ��
 ��1��y����x2��9x(0��x��4)����2����PBQ����������ֵ��20cm2.
�������������������1���ֱ��ʾ��PB��BQ�ij���Ȼ����������ε������ʽ��ʽ�������ɵý⣻
��2���Ѻ�����ϵʽ�����ɶ���ʽ����ʽ��Ȼ����ݶ��κ�������ֵ������
�����������1����S��PBQ��PB��BQ��
PB��AB��AP��18��2x��
BQ��x��
��y�� (18��2x)x��...
��1��y����x2��9x(0��x��4)����2����PBQ����������ֵ��20cm2.
�������������������1���ֱ��ʾ��PB��BQ�ij���Ȼ����������ε������ʽ��ʽ�������ɵý⣻
��2���Ѻ�����ϵʽ�����ɶ���ʽ����ʽ��Ȼ����ݶ��κ�������ֵ������
�����������1����S��PBQ��PB��BQ��
PB��AB��AP��18��2x��
BQ��x��
��y�� (18��2x)x��... ��ѡ��һ����ϲ����a��b��c��ֵ��ʹ���κ���y��ax2��bx��c(a��0)��ͼ��ͬʱ��������������(1)�������£�(2)��x��2ʱ��y��x�����������x��2ʱ��y��x���������С�������Ķ��κ����Ľ���ʽ������____________.
 �𰸲�Ψһ��ֻҪ����b����4a��a��0���ɣ���y����x2��4x��3��y����2x2��8x��3�ȣ�
�������������������ϸ��������Ҫ����ݶ��κ��������ʼ��ɵõ����.
�𰸲�Ψһ����y����(x��1)2��y����(x��1)2��2��
�𰸲�Ψһ��ֻҪ����b����4a��a��0���ɣ���y����x2��4x��3��y����2x2��8x��3�ȣ�
�������������������ϸ��������Ҫ����ݶ��κ��������ʼ��ɵõ����.
�𰸲�Ψһ����y����(x��1)2��y����(x��1)2��2�� ������y��2(x��3)2��1�Ķ���������( )
A. (3��1) B. (3����1) C. (��3��1) D. (��3����1)
 A
�����������������߶���ʽ���ص�ֱ��д�����������ǣ�h��k������֪������y��2(x��3)2��1�Ķ��������ǣ�3��1����
��ѡ��A��
A
�����������������߶���ʽ���ص�ֱ��д�����������ǣ�h��k������֪������y��2(x��3)2��1�Ķ��������ǣ�3��1����
��ѡ��A�� �ڶ��κ�����y��3x2����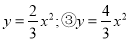 �У�ͼ����ͬһˮƽ���ϵĿ��ڴ�С˳������ű�ʾӦ��Ϊ( )
�У�ͼ����ͬһˮƽ���ϵĿ��ڴ�С˳������ű�ʾӦ��Ϊ( )
A. �٣��ڣ��� B. �٣��ۣ���
C. �ڣ��ۣ��� D. �ڣ��٣���
 C
�����������ݶ��κ��������ʣ���֪ϵ��a�������ڷ���Ϳ��ڴ�С����a��ֵԽ��ԽС����˿�֪�ڣ��ۣ���.
��ѡ��C.
C
�����������ݶ��κ��������ʣ���֪ϵ��a�������ڷ���Ϳ��ڴ�С����a��ֵԽ��ԽС����˿�֪�ڣ��ۣ���.
��ѡ��C. 
