题目内容
如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y=| k |
| x |
考点：相似三角形的判定与性质,反比例函数系数k的几何意义
专题：几何图形问题
分析：证△DCO∽△ABO，推出
=
=
=
，求出
=（
）2=
，求出S△ODC=8，根据三角形面积公式得出
OC×CD=8，求出OC×CD=16即可．
| DC |
| AB |
| OC |
| OB |
| OD |
| OA |
| 2 |
| 3 |
| S△ODC |
| S△OAB |
| 2 |
| 3 |
| 4 |
| 9 |
| 1 |
| 2 |
解答：解：∵OD=2AD，
∴
=
，
∵∠ABO=90°，DC⊥OB，
∴AB∥DC，
∴△DCO∽△ABO，
∴
=
=
=
，
∴
=（
）2=
，
∵S四边形ABCD=10，
∴S△ODC=8，
∴
OC×CD=8，
OC×CD=16，
∴k=-16，
故答案为：-16．
∴
| OD |
| OA |
| 2 |
| 3 |
∵∠ABO=90°，DC⊥OB，
∴AB∥DC，
∴△DCO∽△ABO，
∴
| DC |
| AB |
| OC |
| OB |
| OD |
| OA |
| 2 |
| 3 |
∴
| S△ODC |
| S△OAB |
| 2 |
| 3 |
| 4 |
| 9 |
∵S四边形ABCD=10，
∴S△ODC=8，
∴
| 1 |
| 2 |
OC×CD=16，
∴k=-16，
故答案为：-16．
点评：本题考查了反比例函数图象上点的坐标特征，相似三角形的性质和判定的应用，解此题的关键是求出△ODC的面积．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
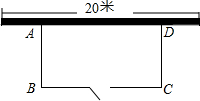某养鸡专业户计划用一段长为35米的竹篱笆围成一个一边靠墙的矩形养鸡场地，如图，墙长20米，BC边有一个宽为1米的木门（木门用其它材料做不点用竹篱笆）．设养鸡场AB边的长为x米，BC边的长为y米，BC的长度不小于10米且不超过墙长．求y关于x的函数解析式及x的取值范围．
画出一次函数y=-2x+4的图象，并回答：当函数值为正时，x的取值范围是
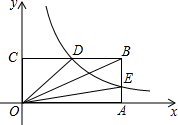如图，在平面直角坐标系中，点O为坐标系原点，矩形OABC的边OA，OC分别在x轴和y轴上，其中OA=6，OC=3．已知反比例函数y=
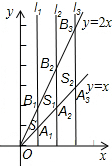如图，直线l1⊥x轴于点（1，0），直线l2⊥x轴于点（2，0），直线l3⊥x轴于点（3，0），…直线ln⊥x轴于点（n，0）．函数y=x的图象与直线l1，l2，l3…ln分别交于点A1，A2，A3，…An；函数y=2x的图象与直线l1，l2，l3…ln分别交于点B1，B2，B3…Bn，如果△OA1B1的面积记作S1，四边形A1A2B2B1的面积记作S2，四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn，那么S2014=