题目内容
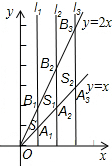 如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3…ln分别交于点B1,B2,B3…Bn,如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn,那么S2014=
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3…ln分别交于点B1,B2,B3…Bn,如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3…四边形An-1AnBnBn-1的面积记作Sn,那么S2014=考点:一次函数图象上点的坐标特征
专题:规律型
分析:根据直线解析式求出An-1Bn-1,AnBn的值,再根据直线ln-1与直线ln互相平行并判断出四边形An-1AnBn Bn-1是梯形,然后根据梯形的面积公式求出Sn的表达式,然后把n=2014代入表达式进行计算即可得解.
解答:解:根据题意,An-1Bn-1=2(n-1)-(n-1)=2n-2-n+1=n-1,
AnBn=2n-n=n,
∵直线ln-1⊥x轴于点(n-1,0),直线ln⊥x轴于点(n,0),
∴An-1Bn-1∥AnBn,且ln-1与ln间的距离为1,
∴四边形An-1AnBn Bn-1是梯形,
Sn=
(n-1+n)×1=
(2n-1),
当n=2014时,S2014=
(2×2014-1)=2013.5.
故答案为:2013.5.
AnBn=2n-n=n,
∵直线ln-1⊥x轴于点(n-1,0),直线ln⊥x轴于点(n,0),
∴An-1Bn-1∥AnBn,且ln-1与ln间的距离为1,
∴四边形An-1AnBn Bn-1是梯形,
Sn=
| 1 |
| 2 |
| 1 |
| 2 |
当n=2014时,S2014=
| 1 |
| 2 |
故答案为:2013.5.
点评:本题是对一次函数的综合考查,读懂题意,根据直线解析式求出An-1Bn-1,AnBn的值是解题的关键,要注意脚码的对应关系,这也是本题最容易出错的地方.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
要使两点P1(x1,y1)、P2(x2,y2)都在平行于y轴的某一直线上,那么必须满足( )
| A、x1=x2 |
| B、y1=y2 |
| C、|x1|=|y2| |
| D、|y1|=|y2| |
 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y= 如图是一个几何体的三视图,这个几何体是
如图是一个几何体的三视图,这个几何体是 如图,等腰梯形ABCD的周长为16,BC=4,CD=3,则AB=
如图,等腰梯形ABCD的周长为16,BC=4,CD=3,则AB= 如图,AB是⊙O的直径,点D在⊙O上,∠BOD=130°,AC∥OD交⊙O于点C,连接BC,则∠B=
如图,AB是⊙O的直径,点D在⊙O上,∠BOD=130°,AC∥OD交⊙O于点C,连接BC,则∠B= 如图,在菱形ABCD中,AB=2
如图,在菱形ABCD中,AB=2
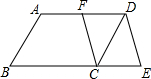 如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=
如图,在?ABCD中,F是AD的中点,延长BC到点E,使CE=