Question

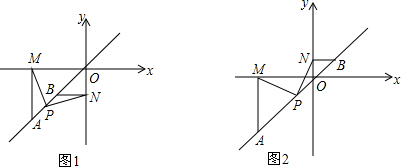
如图，已知点A，点B在第一，三象限的角平分线上，P为直线AB上的一点，PA=PB，AM、BN分别垂直与x轴、y轴，连接PM、PN．
（1）求直线AB的解析式；
（2）如图1，P、A、B在第三象限，猜想PM，PN之间的关系，并说明理由；
（3）点P、A在第三象限，点B在第一象限，如图2其他条件不变，（2）中的结论还成立吗，请证明你的结论．

Answer 1

考点：一次函数综合题,角平分线的定义,全等三角形的性质,等腰三角形的性质,矩形的判定与性质

专题：几何综合题

分析：（1）根据角平分线性质得出即可；
（2）求出OQ=AQ，OM=OQ，OE=OF，PE=PF，证△MEP≌△NFP，推出PM=PN，∠EPM=∠NPF，求出∠EPF=90°，即可求出∠MPN=∠MPE+∠EPN=∠EPF=90°；
（3）延长BN交AM于E，连接EP，求出ME=ON=BN，∠AEB=90°，根据直角三角形性质求出∠MEP=∠NBP=45°，EP=PB，∠EPB=90°，证△EMP≌△BNP，推出PM=PN，∠EPM=∠NPB，求出∠MPN=∠EPB=90°，即可得出答案．

解答：解：（1）∵点A，点B在第一，三象限的角平分线上，
∴直线AB的解析式是y=x；

（2）PM=PN且PM⊥PN，
理由是：过P作PE⊥x轴于E，PF⊥y轴于F，过A作AQ⊥y轴于Q，
∵A在第一、三象限的角平分线上，PM⊥x轴于M，
∴AM=AQ，∠AMO=90°，∠MOA=45°，
∴∠MAO=∠MOA=45°，
∴OM=AM，
同理OQ=AQ，
∴OM=OQ，
同理OE=OF，PE=PF，
在△MEP和△NFP中

ME=NF ∠MEP=∠NFP=90° PE=PF

∴△MEP≌△NFP（SAS），
∴PM=PN，∠EPM=∠NPF，
∵PE⊥x轴，PF⊥y轴，x轴⊥y轴，
∴∠EOF=∠OEP=∠OFP=90°，
∴∠EPF=90°，
∴∠MPN=∠MPE+∠EPN=∠FPN+∠EPN=∠EPF=90°，
即PM⊥PN；

（3）成立；

证明：延长BN交AM于E，连接EP，
∵A、B在第一、三象限角的角平分线上，
∴∠MOA=∠BON=45°，
∵∠BNO=∠AMO=90°，
∴∠NBO=∠EAO=∠NOB=45°，
∴AE=BE，BN=ON，
∵∠ENO=∠NOM=∠EMO=90°，
∴四边形EMON是矩形，
∴ME=ON=BN，∠AEB=90°，
∵P为AB中点，AE=BE，
∴∠MEP=∠NBP=45°，EP=PB，∠EPB=90°，
在△EMP和△BNP中

EP=BP ∠MEP=∠NBP EM=BN

∴△EMP≌△BNP（SAS），
∴PM=PN，∠EPM=∠NPB，
∵∠EPB=90°，
∴∠MPN=∠MPE+∠EPN=∠BPN+∠EPN=∠EPB=90°，
即PM⊥PN．

点评：本题考查了角平分线性质，全等三角形的性质和判定，等腰三角形性质和判定，矩形的性质和判定的应用，题目综合性比较强，有一定的难度．