题目内容
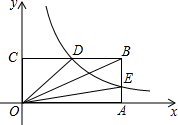 如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数y=
如图,在平面直角坐标系中,点O为坐标系原点,矩形OABC的边OA,OC分别在x轴和y轴上,其中OA=6,OC=3.已知反比例函数y=| k |
| x |
(1)k的值为
(2)猜想△OCD的面积与△OBE的面积之间的关系,请说明理由.
考点:待定系数法求反比例函数解析式,反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,矩形的性质
专题:几何综合题
分析:(1)根据题意得出点D的坐标,从而可得出k的值;
(2)根据三角形的面积公式和点D,E在函数的图象上,可得出S△OCD=S△OAE,再由点D为BC的中点,可得出S△OCD=S△OBD,即可得出结论.
(2)根据三角形的面积公式和点D,E在函数的图象上,可得出S△OCD=S△OAE,再由点D为BC的中点,可得出S△OCD=S△OBD,即可得出结论.
解答:解:∵OA=6,OC=3,点D为BC的中点,
∴D(3,3).
∴k=3×3=9,
故答案为9;
(2)S△OCD=S△OBE,
理由是:∵点D,E在函数的图象上,
∴S△OCD=S△OAE=
,
∵点D为BC的中点,
∴S△OCD=S△OBD,
即S△OBE=
,
∴S△OCD=S△OBE.
∴D(3,3).
∴k=3×3=9,
故答案为9;
(2)S△OCD=S△OBE,
理由是:∵点D,E在函数的图象上,
∴S△OCD=S△OAE=
| 9 |
| 2 |
∵点D为BC的中点,
∴S△OCD=S△OBD,
即S△OBE=
| 9 |
| 2 |
∴S△OCD=S△OBE.
点评:本题考查了用待定系数法求反比例函数的解析式、反比例函数系数k的几何意义、反比例函数图象上点的特征以及矩形的性质,是一道综合题,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险? 已知:如图,正方形ABCD中,E、F分别为AB、BC的中点,CE、DF交于M.
已知:如图,正方形ABCD中,E、F分别为AB、BC的中点,CE、DF交于M.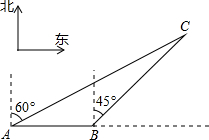 如图:我渔政310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测到我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,离渔船C的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
如图:我渔政310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东60°方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测到我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,离渔船C的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.) 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y= 如图,等腰梯形ABCD的周长为16,BC=4,CD=3,则AB=
如图,等腰梯形ABCD的周长为16,BC=4,CD=3,则AB=