题目内容
4. 佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.根据以上方程与函数的关系,如果我们直到函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象.
| x | … | -3 | -$\frac{5}{2}$ | -2 | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | … |
| y | … | -8 | -$\frac{21}{8}$ | 0 | $\frac{5}{8}$ | m | -$\frac{9}{8}$ | -2 | -$\frac{15}{8}$ | 0 | $\frac{35}{8}$ | 12 | … |
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
分析 (1)求出x=-1时的函数值即可解决问题;利用描点法画出图象即可;
(2)利用图象以及表格即可解决问题;
(3)不等式x3+2x2>x+2的解集,即为函数y=x3+2x2-x-2的函数值大于0的自变量的取值范围,观察图象即可解决问题;
解答 解:(1)由题意m=-1+2+1-2=0.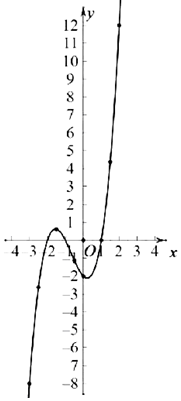
函数图象如图所示.
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1.
故答案为3,-2,或-1或1.
(3)不等式x3+2x2>x+2的解集,即为函数y=x3+2x2-x-2的函数值大于0的自变量的取值范围.
观察图象可知,-2<x<-1或x>1.
点评 本题考查函数与图象的关系,解题的关键是灵活运用所学知识解决问题,学会用转化的思想思考问题,学会利用图象解决一个不等式问题,属于中考常考题型.

练习册系列答案
相关题目
12.|(-3)-5|等于( )
| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
15.已知抛物线L:y=ax2+bx+c与抛物线L′:y=x2-2mx+4m+1关于直线x=2对称,且L′交y轴于点P(0,21),则方程ax2+bx+c=0的两个根为( )
| A. | x1=0,x2=3 | B. | x1=1,x2=-3 | C. | x1=3,x2=7 | D. | x1=-7,x2=-3 |
19.已知双曲线y=$\frac{k}{x}$经过点(m,n),(n+1,m-1),(m2-1,n2-1),则k的值为( )
| A. | 0或3 | B. | 0或-3 | C. | -3 | D. | 3 |
9. 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{4}{{(x-1)}^{2}+1}$的自变量x的取值范围是全体实数;
(2)表格是y与x的几组对应值.
表中m的值为$\frac{2}{5}$;
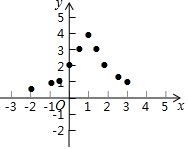
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
根据描出的点,画出函数y=$\frac{4}{{(x-1)}^{2}+1}$的大致图象;
(4)结合函数图象,请写出函数y=$\frac{4}{{(x-1)}^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)如果方程$\frac{4}{{(x-1)}^{2}+1}$=a有2个解,那么a的取值范围是0<a<4.
 小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:
小东根据学习函数的经验,对函数y=$\frac{4}{{(x-1)}^{2}+1}$的图象与性质进行了探究.下面是小东的探究过程,请补充完整,并解决相关问题:(1)函数y=$\frac{4}{{(x-1)}^{2}+1}$的自变量x的取值范围是全体实数;
(2)表格是y与x的几组对应值.
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{3}$ | m | … |
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点.
根据描出的点,画出函数y=$\frac{4}{{(x-1)}^{2}+1}$的大致图象;
(4)结合函数图象,请写出函数y=$\frac{4}{{(x-1)}^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)如果方程$\frac{4}{{(x-1)}^{2}+1}$=a有2个解,那么a的取值范围是0<a<4.
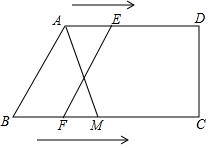 在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
在四边形ABCD中,AD∥BC,BC⊥CD,AD=6cm,BC=10cm,点E从A出发以1cm/s的速度向D运动,点F从点B出发,以2cm/s的速度向点C运动,当其中一点到达终点,而另一点也随之停止,设运动时间为t,
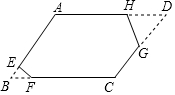 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )