题目内容
14.计算:|-2|-$\root{3}{8}$=0.分析 首先计算开方,然后计算减法,求出算式的值是多少即可.
解答 解:|-2|-$\root{3}{8}$
=2-2
=0
故答案为:0.
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
4. 佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象.
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
 佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.根据以上方程与函数的关系,如果我们直到函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象.
| x | … | -3 | -$\frac{5}{2}$ | -2 | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | … |
| y | … | -8 | -$\frac{21}{8}$ | 0 | $\frac{5}{8}$ | m | -$\frac{9}{8}$ | -2 | -$\frac{15}{8}$ | 0 | $\frac{35}{8}$ | 12 | … |
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
5.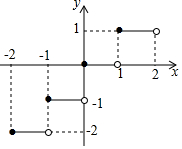 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )
定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )
 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )
定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=$\frac{1}{2}$x2的解为( )| A. | 0或$\sqrt{2}$ | B. | 0或2 | C. | 1或$-\sqrt{2}$ | D. | $\sqrt{2}$或-$\sqrt{2}$ |
2. 如图所示的立方体,如果把它展开,可以是下列图形中的( )
如图所示的立方体,如果把它展开,可以是下列图形中的( )
 如图所示的立方体,如果把它展开,可以是下列图形中的( )
如图所示的立方体,如果把它展开,可以是下列图形中的( )| A. |  | B. |  | C. |  | D. |  |
19.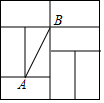 如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )
如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )
 如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )
如图是由8个全等的矩形组成的大正方形,线段AB的端点都在小矩形的顶点上,如果点P是某个小矩形的顶点,连接PA、PB,那么使△ABP为等腰直角三角形的点P的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.用量角器测得∠MON的度数,下列操作正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
3.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )
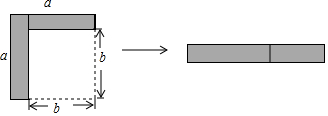

| A. | (a-b)2=a2-2ab+b2 | B. | a(a-b)=a2-ab | C. | (a-b)2=a2-b2 | D. | a2-b2=(a+b)(a-b) |
4.下列计算正确的是( )
| A. | 4a2-2a2=2 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | (2a2)3=6a6 |
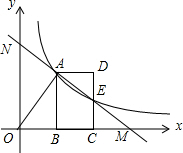 如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.