题目内容
12.|(-3)-5|等于( )| A. | -8 | B. | -2 | C. | 2 | D. | 8 |
分析 根据分式的减法和绝对值可以解答本题.
解答 解:|(-3)-5|
=|-3-5|
=|-8|
=8,
故选D.
点评 本题考查有理数的减法和绝对值,解答本题的关键是明确有理数减法的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.观察以下一列数的特点:0,1,-4,9,-16,25,…,则第11个数是( )
| A. | -121 | B. | -100 | C. | 100 | D. | 121 |
7.若实数3是不等式2x-a-2<0的一个解,则a可取的最小正整数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
4. 佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象.
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
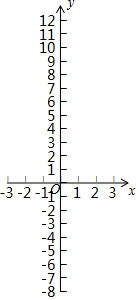 佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.
佳佳向探究一元三次方程x3+2x2-x-2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2-2x-3的图象与x轴的交点为(-1,0)和(3,0),交点的横坐标-1和3即为x2-2x-3=0的解.根据以上方程与函数的关系,如果我们直到函数y=x3+2x2-x-2的图象与x轴交点的横坐标,即可知方程x3+2x2-x-2=0的解.
佳佳为了解函数y=x3+2x2-x-2的图象,通过描点法画出函数的图象.
| x | … | -3 | -$\frac{5}{2}$ | -2 | -$\frac{3}{2}$ | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | … |
| y | … | -8 | -$\frac{21}{8}$ | 0 | $\frac{5}{8}$ | m | -$\frac{9}{8}$ | -2 | -$\frac{15}{8}$ | 0 | $\frac{35}{8}$ | 12 | … |
(2)根据表格和图象可知,方程的解有3个,分别为-2,或-1或1;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.
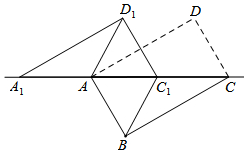 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论: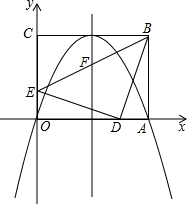 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).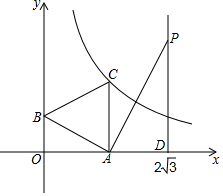 如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
如图,一次函数y=-$\frac{{\sqrt{3}}}{3}$x+1的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.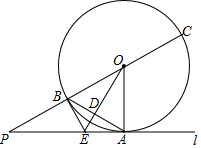 如图,直线1与⊙O相切于点A,点P在直线1上,直线PO交⊙O于点B、C,OD⊥AB,垂足为D,交PA于点E.
如图,直线1与⊙O相切于点A,点P在直线1上,直线PO交⊙O于点B、C,OD⊥AB,垂足为D,交PA于点E.