题目内容
7.在三角形ABC中,∠ABC等于90度,AB=6,BC=8,AC=10,BD平分∠ABC交AC于D,求CD长( )| A. | $\frac{20}{7}$ | B. | $\frac{30}{7}$ | C. | $\frac{40}{7}$ | D. | 无法确定 |
分析 过D作DM⊥AB于M,DN⊥BC于N,得到四边形BNDM是矩形,根据角平分线的性质得到DM=DN,推出矩形BNDM是正方形,得到DM=BM=BN=DN=x,根据相似三角形的性质即可得到结论.
解答  解:过D作DM⊥AB于M,DN⊥BC于N,
解:过D作DM⊥AB于M,DN⊥BC于N,
∵∠ABC=90°,
∴四边形BNDM是矩形,
∵BD平分∠ABC交AC于D,
∴DM=DN,
∴矩形BNDM是正方形,
∴DM=BM=BN=DN,
设DM=BM=BN=DN=x,
则CN=8-x,
∵DN⊥BC,AB⊥BC,
∴DN∥AB,
∴△CDN∽△CBA,
∴$\frac{CN}{BC}$=$\frac{DN}{AB}$=$\frac{CD}{AC}$,
即$\frac{8-x}{8}$=$\frac{x}{6}$=$\frac{CD}{10}$,
∴CD=$\frac{40}{7}$,
故选C.
点评 本题考查了角平分线的性质,正方形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
18. 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )
 如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )
如图,多边形的相邻两边均互相垂直,则这个多边形的周长为( )| A. | a+b | B. | 2a+b | C. | 2(a+b) | D. | a+2b |
16.下列条件中,不能判定两个直角三角形全等的是( )
| A. | 两直角边对应相等 | B. | 斜边和一条直角边对应相等 | ||
| C. | 两锐角对应相等 | D. | 一个锐角和斜边对应相等 |
17.若把分式$\frac{x+y}{2x+y}$中的x和y都扩大3倍,且x+y≠0,那么分式的值( )
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 缩小6倍 |
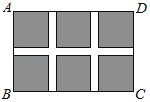 如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm.
如图,某小区规划在一个长30m,宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,设通道的宽为xm. 如图1,图2均为3×3方格,在图1中,已知各行、各列及对角线上三个数之和都等于15,试求x、y的值,并把满足已知条件的另外8个数字填入图2的方格内.
如图1,图2均为3×3方格,在图1中,已知各行、各列及对角线上三个数之和都等于15,试求x、y的值,并把满足已知条件的另外8个数字填入图2的方格内.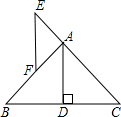 如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由.
如图,在△ABC中,AB=AC,E在CA延长线上,AE=AF,AD是高,试判断EF与BC的位置关系,并说明理由. 如图,已知:△ABC中,AD与BE相交于F,且AE=EC,BD:DC=1:2,求:BF:FE.
如图,已知:△ABC中,AD与BE相交于F,且AE=EC,BD:DC=1:2,求:BF:FE.