题目内容

19．如图，已知：△ABC中，AD与BE相交于F，且AE=EC，BD：DC=1：2，求：BF：FE．

分析 作EH∥BC交AD于H，如图，先利用EH∥CD得到EH：CD=AE：AC=1：2，则利用BD：DC=1：2得到EH=BD，然后根据平行线分线段成比例定理，由EH∥BD可得到BF：FE的比值．

解答 解：作EH∥BC交AD于H，如图，
∵EH∥CD，
∴EH：CD=AE：AC=1：2，
∵BD：DC=1：2，
∴EH=BD，
∵EH∥BD，
∴EH：BD=EF：BF=1：1，
即BF：FE=1：1．

点评 本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例．

练习册系列答案
相关题目
9．如图，图1和图2都是有边长为2的正方形和以正方形顶点为圆心、正方形的边长为半径的圆弧组成的图形．
（1）计算图1中阴影部分的面积；
（2）图2中的阴影部分面积与图1中的阴影部分的面积相等．（填“相等”或“不相等”）
（3）图3是一个圆心角45°、半径为2的扇形和一个等腰直角三角形的图形，那么图中的阴影部分面积是$\frac{π}{4}$-1．
（4）图4是一个由等腰直角三角形和以三角形的顶点为圆心、直角边长为半径的圆弧组成的图形，求阴影部分的面积．
10．平面直角坐标系中，A（-2，6）、B（2，2）
（1）如图1，连接AO、BO，求△ABO的面积；
（2）如图2，在x轴上是否存在点P，使△ABP的面积等于6？若存在，求P点坐标；若不存在，请说明理由．
（3）如图3，延长AB交x轴于D，将AD绕点A顺时针旋转30°，它的延长线交y轴负半轴于点E，在第四象限的点F．使得x轴、y轴分别平分∠ADF、∠AEF，试求∠DFE的值．
7．在三角形ABC中，∠ABC等于90度，AB=6，BC=8，AC=10，BD平分∠ABC交AC于D，求CD长（　　）
A．$\frac{20}{7}$B．$\frac{30}{7}$C．$\frac{40}{7}$D．无法确定
14．我们做一次眼保健操大约需要5分钟，每天做两次．我们每天做眼保健操的时间大约占1小时的$\frac{1}{6}$．
4．某条抛物线向左平移1个单位，再向上平移2个单位后，所得到的方程是y=x2，那么原抛物线方程为（　　）
A．y=（x+1）2+2B．y=（x+1）2-2C．y=（x-1）2+2D．y=（x-1）2-2
11．已知A-2B=7a2-7ab，且B=-4a2+6ab+7．
（1）用含a，b的代数式表示A．
（2）若|a+1|+（b-2）2=0，求A的值．
8．有一个两位数，它的两个数字之和为11，把这个两位数的个位数字与十位数字对调，所得的新数比原数大63，设原两位数的个位数字为x，十位数字为y，根据题意，得方程组$\left\{\begin{array}{l}{x+y=11}\\{10x+y-（10y+x）=63}\end{array}\right.$．
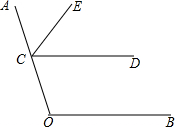9．如图，点C在射线OA上，CE平分∠ACD．OF平分∠COB并与射线CD交于点F．
（1）依题意补全图形；
（2）若∠COB+∠OCD=180°，求证：∠ACE=∠COF．
请将下面的证明过程补充完整．
证明：∵CE平分∠ACD，OF平分∠COB，
∴∠ACE=$\frac{1}{2}$∠ACD，∠COF=$\frac{1}{2}$∠COB．
（理由：角平分线的定义）
∵点C在射线OA上，
∴∠ACD+∠OCD=180°．
∵∠COB+∠OCD=180°，
∴∠ACD=∠COB．
（理由：同角的补角相等）
∴∠ACE=∠COF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网