题目内容
11. 如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )
如图,已知菱形ABCD对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是( )| A. | 5$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
分析 首先利用菱形的性质结合勾股定理得出BC的长,再利用三角形面积求出答案.
解答 解:∵四边形ABCD是菱形,AC=6cm,BD=8cm,
∴AO=CO=3cm,BO=DO=4cm,∠BOC=90°,
∴BC=$\sqrt{{4}^{2}+{3}^{2}}$=5(cm),
∴AE×BC=BO×AC
故5AE=24,
解得:AE=$\frac{24}{5}$.
故选:C.
点评 此题主要考查了菱形的性质以及勾股定理,正确得利用三角形面积求出AE的长是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.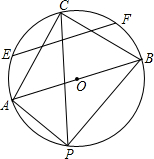 如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
 如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )
如图,AB是半径为4的⊙O的直径,P是圆上异于A,B的任意一点,∠APB的平分线交⊙O于点C,连接AC和BC,△ABC的中位线所在的直线与⊙O相交于点E、F,则EF的长是( )| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 6 | D. | 2$\sqrt{5}$ |
3.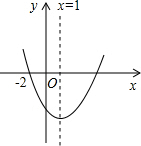 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )
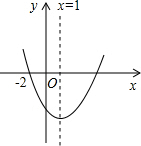 如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )
如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①b<0;②b+2a=0;③方程ax2+bx+c=0的两个根为x1=-2,x2=4;④a+c>b;⑤3a+c<0.其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
1. 如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
 如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )
如图,AB是⊙O的直径,CD是⊙O上的点,∠DCB=30°,过点D作⊙O的切线交AB的延长线于E,若AB=4,则DE的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
 [实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.
[实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍. 如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点.
如图,已知一次函数y=ax-2的图象与反比例函数y=$\frac{k}{x}$的图象交于A(k,a),B两点. 小明家国庆期间租车到某地旅游,先匀速行驶50千米的普通公路,这时油箱内余油32升,由于国庆期间高速免费,进而上高速公路匀速行驶到达旅游目的地.如图是汽车油箱内余油量Q(升)与行驶路程s(千米)之间的函数图象,当行驶150千米时油箱内余油26升.
小明家国庆期间租车到某地旅游,先匀速行驶50千米的普通公路,这时油箱内余油32升,由于国庆期间高速免费,进而上高速公路匀速行驶到达旅游目的地.如图是汽车油箱内余油量Q(升)与行驶路程s(千米)之间的函数图象,当行驶150千米时油箱内余油26升.