题目内容
8.在Rt△ABC中,CD是斜边AB上的高,若AD:BD=1:3,求△ACD与△ABC的周长之比.分析 在Rt△ABC中,CD是斜边AB上的高,于是得到∠ADC=∠ACB=∠BDC=90°,求得∠A=∠BCD,推出△ACD∽△BCD,根据相似三角形的性质得到$\frac{CD}{AD}=\frac{BD}{CD}$,由已知条件设AD=k,BD=3k,得到CD=$\sqrt{3}$k,根据勾股定理求得AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=2k,AB=4k,通过△ACD∽△ABC,根据相似三角形的性质即可得到结论.
解答 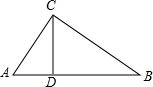 解:如图,在Rt△ABC中,CD是斜边AB上的高,
解:如图,在Rt△ABC中,CD是斜边AB上的高,
∴∠ADC=∠ACB=∠BDC=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△BCD,
∴$\frac{CD}{AD}=\frac{BD}{CD}$,
∵AD:BD=1:3,
∴设AD=k,BD=3k,
∴CD=$\sqrt{3}$k,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=2k,AB=4k,
∵∠A=∠A,
∴△ACD∽△ABC,
∴△ACD与△ABC的周长之比=$\frac{AC}{AB}$=$\frac{1}{2}$.
点评 本题主要考查相似三角形的判定和性质,掌握相似三角形的判定方法是解题的关键,注意线段的比例和乘积的互化.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
2.2015年2月1日,石家庄市区的最高气温是2℃,最低气温是-5℃,则该天的最高气温比最低气温高( )
| A. | -7℃ | B. | 7℃ | C. | -3℃ | D. | 3℃ |
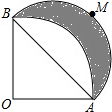 如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.
如图,AB=2cm,∠AOB=90°,OA=OB,以OA为半径作$\widehat{AB}$,以AB为半径作半圆$\widehat{AMB}$,则$\widehat{AMB}$和$\widehat{AB}$所围成的阴影部分面积为1cm2.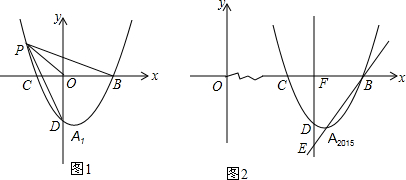
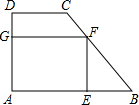 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.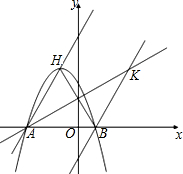 已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$对称.
已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$对称.