题目内容
19．计算$\frac{x}{x+1}+\frac{2x}{{x}^{2}-1}$的结果为$\frac{x}{x-1}$．分析 原式通分并利用同分母分式的加法法则计算，即可得到结果．
解答 解：原式=$\frac{x（x-1）+2x}{（x+1）（x-1）}$=$\frac{x（x+1）}{（x+1）（x-1）}$=$\frac{x}{x-1}$，
故答案为：$\frac{x}{x-1}$
点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
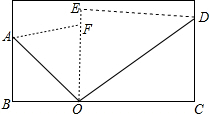将一张矩形纸片按如图方式折叠，设O点是矩形边上一点，将矩形的一角沿OA翻折使OB与OF重合，再将其邻角沿0D翻折，使OC与OE重合，且O、E、F在同一直线上．求OA与∠BOF、OD与∠EOC的关系．
表示a-b+c，图形
表示-x+y-z，则
+
的值为-3．
14．计算$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}y+x{y}^{2}}$$•\frac{xy}{x-y}$的结果为（ ）
| A． | $\frac{x-y}{x+y}$ | B． | $\frac{x+y}{x-y}$ | C． | $\frac{（x-y）^{2}}{x+y}$ | D． | 1 |
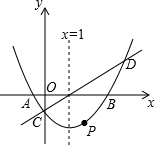如图，在直角坐标系中，抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A，B两点，与y轴交于点C，且对称轴是直线x=1．直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C，D两点．点P是抛物线上的动点．
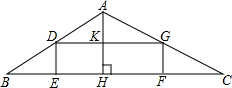如图，矩形DEFG内接于△ABC，AH⊥BC，DG与AH相交于点K，BC=48，高AH=16．