题目内容
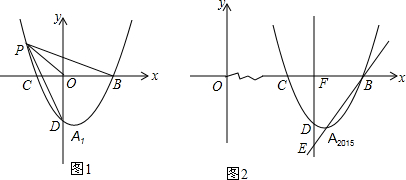
3.已知抛物线y=x2+bx+c,点An(an,-4)为抛物线的顶点,且a1=1,an+1=an+1(n>0).以A1为顶点的抛物线记为C1,以A2为顶点的抛物线记为C2,…以An为顶点的抛物线记为Cn.(1)求C1抛物线的解析式;
(2)C1与x轴交于点B、C两点(B在C点的右侧),抛物线上是否存在一点P,使△POB与△POD全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)C2015与x轴交于B、C两点,直线x=2014与C2015、直线A2015B、x轴分别交于D、E、F点,判断以线段A2015B为直径的圆与直线x=2014的位置关系?并说明理由.
分析 (1)根据顶点坐标,可得方程组,根据解方程组,可得答案;
(2)根据三边对应相等的两个三角形全等,可得PB=PD,根据方程,可得答案;
(3)根据an+1=an+1,可得A2015坐标,根据图象平移规律,可得B点,根据线段中点公式,可得A2015B的中点,根据到与直线的距离,可得圆心到直线的距离,根据勾股定理,可得A2015B的长,根据圆心到直线的距离小于半径,可得答案.
解答 解:(1)a1=1,故C1的顶点为(1,-4),
$\left\{\begin{array}{l}{-\frac{b}{2}=1}\\{\frac{4c-{b}^{2}}{4}=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$,
所以y=x2-2x-3;
(2)设P(x,(x-1)2-4),当x=0时,y=-3,即D(0,-3),
当y=0时,x2-2x-3=0,解得x=3或x=-1,即B(3,0),
OB=OD,PO=PO,当PB=PD时,△POB≌△POD,
(x-3)2+[(x-1)2-4]2=x2+[(x-1)2-4+3]2,
化简,得x2-x-3=0,
解得x1=$\frac{1+\sqrt{13}}{2}$,x2=$\frac{1-\sqrt{13}}{2}$,
y1=$\frac{-1-\sqrt{13}}{2}$,y2=$\frac{-1+\sqrt{13}}{2}$,
P1($\frac{1+\sqrt{13}}{2}$,$\frac{-1-\sqrt{13}}{2}$),P2($\frac{1-\sqrt{13}}{2}$,$\frac{-1+\sqrt{13}}{2}$);
(3)A2015(2015,-4),B(2017,0),A2015B的中点O(2016,-2)
O到直线x=2014距离为2016-2014=2,
而圆的半径为$\frac{{A}_{2015}B}{2}$=$\frac{\sqrt{(2017-2015)^{2}+(0+4)^{2}}}{2}$=$\sqrt{5}$
因为2<$\sqrt{5}$,
所以x=2014与圆相交.
点评 本题考查了二次函数综合题,(1)利用顶点坐标公式得出方程组是解题关键;(2)利用三角形全等的条件得出PB=PD是解题关键;(3)利用图象平移规律得出A2015、B点坐标是解题关键,又利用了直线与圆的位置关系.

| A. | $\frac{x-y}{x+y}$ | B. | $\frac{x+y}{x-y}$ | C. | $\frac{(x-y)^{2}}{x+y}$ | D. | 1 |
| A. | 2a+3 | B. | $\frac{a}{2}$-1 | C. | $\frac{1}{5}$a2-2a+10 | D. | $\frac{7{a}^{2}-100}{5}$ |
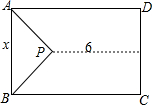 如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.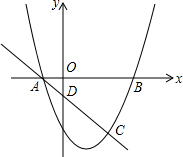 抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).
抛物线y=ax2+bx+c与x轴的交点为A(-1,0)和B(3,0),与直线y=-x+k相交于点A和点C(2,-3).